题目内容
用配方法解下列方程:
(1)2x2-5x-7=0;
(2)
y2-y-
=0;
(3)(x+1)(x-1)=2x2-4x-6.
(1)2x2-5x-7=0;
(2)
| 3 |
| 3 |
(3)(x+1)(x-1)=2x2-4x-6.
考点:解一元二次方程-配方法
专题:计算题
分析:各方程二次项系数化为1,常数项移到右边,两边加上一次项系数一半的平方,利用完全平方公式变形后,开方即可求出解.
解答:解:(1)方程变形得:x2-
x=
,
配方得:x2-
x+
=
+
,即(x-
)2=
,
开方得:x-
=±
,
解得:x1=
,x2=-1;
(2)方程变形得:y2-
y=19,
配方得:y2-
y+
=
,即(y-
)2=
,
开方得:y-
=±
,
解得:y=
;
(3)整理得:x2-4x=5,
配方得:x2-4x+4=9,即(x-2)2=9,
开方得:x-2=±3,
解得:x1=5,x2=-1.
| 5 |
| 2 |
| 7 |
| 2 |
配方得:x2-
| 5 |
| 2 |
| 25 |
| 16 |
| 7 |
| 2 |
| 25 |
| 16 |
| 5 |
| 4 |
| 81 |
| 16 |
开方得:x-
| 5 |
| 4 |
| 9 |
| 4 |
解得:x1=
| 7 |
| 2 |
(2)方程变形得:y2-
| 1 | ||
|
配方得:y2-
| 1 | ||
|
| 1 |
| 12 |
| 13 |
| 12 |
| 1 | ||
2
|
| 13 |
| 12 |
开方得:y-
| 1 | ||
2
|
|
解得:y=
| ||||
| 6 |
(3)整理得:x2-4x=5,
配方得:x2-4x+4=9,即(x-2)2=9,
开方得:x-2=±3,
解得:x1=5,x2=-1.
点评:此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知,△ABC中,AB=AC,在AB上取一点D,在AC延长线上取一点E,连接DE交BC于点F.若F是DE中点,求证:BD=CE.
已知,△ABC中,AB=AC,在AB上取一点D,在AC延长线上取一点E,连接DE交BC于点F.若F是DE中点,求证:BD=CE. 如图,有一块呈三角形形状的草坪,其中一边的长是20m,在这个草坪的图纸上,这条边长是5cm,其他两边的长度都是3.5cm,求该草坪其他两边的实际长度.
如图,有一块呈三角形形状的草坪,其中一边的长是20m,在这个草坪的图纸上,这条边长是5cm,其他两边的长度都是3.5cm,求该草坪其他两边的实际长度.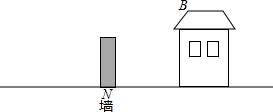 如图,小区管理者打算在广场的地面上安装一盏路灯(路灯高度忽略不计).小明此刻正在某建筑物的B处向下看,请问:此路灯安在什么位置,小明在B处看不到?请把这段范围用线段表示出来.
如图,小区管理者打算在广场的地面上安装一盏路灯(路灯高度忽略不计).小明此刻正在某建筑物的B处向下看,请问:此路灯安在什么位置,小明在B处看不到?请把这段范围用线段表示出来. 如图,已知△ABC∽△DEF,求未知边x,y的长度.
如图,已知△ABC∽△DEF,求未知边x,y的长度. 如图所示,在平行四边形ABCD中,∠A=60°,CD=BC,E,F分别在AB和BC上,且∠EDF=60°.
如图所示,在平行四边形ABCD中,∠A=60°,CD=BC,E,F分别在AB和BC上,且∠EDF=60°.