题目内容
9.当x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为2或$-\sqrt{3}$.分析 求出二次函数对称轴为直线x=m,再分m≤1,m>两种情况,根据二次函数的增减性列方程求解即可.
解答 解:二次函数对称轴为直线x=m,
①m≤1时,x=m取得最大值,m2+1=4,
解得m=±$\sqrt{3}$,
∵m=$\sqrt{3}$都不满足-1≤m≤1的范围,
∴m=-$\sqrt{3}$;
②m>1时,x=1取得最大值,-(1-m)2+m2+1=4,
解得m=2.
综上所述,m=-$\sqrt{3}$或2时,二次函数有最大值4.
故答案为:2或$-\sqrt{3}$.
点评 本题考查了二次函数的最值,熟悉二次函数的性质及图象是解题的关键.

练习册系列答案
相关题目
4.某市2015年国内生产总值(GDP)比2014年增长了12%,预计2016年比2015年增长7%,若这两年GDP年平均增长率为x%,则x%满足的关系是( )
| A. | 12%+7%=x% | B. | (1+12%)(1+7%)=2(1+x%) | C. | 12%+7%=2x% | D. | (1+12%)(1+7%)=(1+x%)2 |
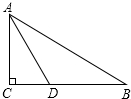 如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=10cm,BD=5cm,那么D点到直线AB的距离是5cm.
如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=10cm,BD=5cm,那么D点到直线AB的距离是5cm. 在数学活动课上,老师带领学生去测量操场上树立的旗杆的高度,老师为同学们准备了如下工具:①高为m米的测角仪,②长为n米的竹竿,③足够长的皮尺.请你选用以上的工具,设计一个可以通过测量,求出国旗杆高度的方案(不用计算和说明,画出图形并标记可以测量的长度或者角度即可,可测量的角度选用α,β,γ标记,可测量的长度选用a,b,c,d标记,测角仪和竹竿可以用线段表示).
在数学活动课上,老师带领学生去测量操场上树立的旗杆的高度,老师为同学们准备了如下工具:①高为m米的测角仪,②长为n米的竹竿,③足够长的皮尺.请你选用以上的工具,设计一个可以通过测量,求出国旗杆高度的方案(不用计算和说明,画出图形并标记可以测量的长度或者角度即可,可测量的角度选用α,β,γ标记,可测量的长度选用a,b,c,d标记,测角仪和竹竿可以用线段表示).