题目内容
已知:关于x的方程x2-(k+3)x+3k=0的两根为α,β.
(1)是否存在实数k使
+
=
成立?若成立,求k的值;若不成立,说明理由;
(2)若Rt△ABC的一边长为4,另两边长恰好是此方程的两根α,β,求Rt△ABC的周长.
(1)是否存在实数k使
| 1 |
| α |
| 1 |
| β |
| 2 |
| 3 |
(2)若Rt△ABC的一边长为4,另两边长恰好是此方程的两根α,β,求Rt△ABC的周长.
考点:根与系数的关系,根的判别式,勾股定理
专题:
分析:(1)根据根与系数的关系得到α+β=k+3,αβ=-3k,再由
+
=
变形得
=
,所以
=
,然后解方程求出k的值;
(2)先利用因式分解法解方程x2-(k+3)x+3k=0得α=k,β=3,然后分类讨论:当4为斜边或当4为直角边,根据勾股定理建立等量关系求出对应的k的值,再计算三角形的周长.
| 1 |
| α |
| 1 |
| β |
| 2 |
| 3 |
| α+β |
| αβ |
| 2 |
| 3 |
| k+3 |
| -3k |
| 2 |
| 3 |
(2)先利用因式分解法解方程x2-(k+3)x+3k=0得α=k,β=3,然后分类讨论:当4为斜边或当4为直角边,根据勾股定理建立等量关系求出对应的k的值,再计算三角形的周长.
解答:解:(1)存在.
∵α+β=k+3,αβ=-3k,
而
+
=
,
∴
=
,
∴
=
,解得k=-1,
当k=-1时△>0,
∴实数k=1使
+
=
成立;
(2)解方程x2-(k+3)x+3k=0得α=k,β=3,
当4为斜边时,α2+β2=42,即k2+32=16,解得k1=
,k2=-
(舍去),此时Rt△ABC的周长=4+3+
=7+
;
当4为直角边时,42+β2=k2,即k2+32=16,解得k1=5,k2=-5(舍去),此时Rt△ABC的周长=4+3+5=12.
∵α+β=k+3,αβ=-3k,
而
| 1 |
| α |
| 1 |
| β |
| 2 |
| 3 |
∴
| α+β |
| αβ |
| 2 |
| 3 |
∴
| k+3 |
| -3k |
| 2 |
| 3 |
当k=-1时△>0,
∴实数k=1使
| 1 |
| α |
| 1 |
| β |
| 2 |
| 3 |
(2)解方程x2-(k+3)x+3k=0得α=k,β=3,
当4为斜边时,α2+β2=42,即k2+32=16,解得k1=
| 7 |
| 7 |
| 7 |
| 7 |
当4为直角边时,42+β2=k2,即k2+32=16,解得k1=5,k2=-5(舍去),此时Rt△ABC的周长=4+3+5=12.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了勾股定理.
| b |
| a |
| c |
| a |

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
计算-b2•(-b3)2的结果是( )
| A、-b8 |
| B、-b11 |
| C、b8 |
| D、b11 |
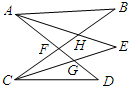 如图,AD、BC相交于点F,AE、CE分别平分∠BAD、∠DCB,若∠B=25°,∠D=35°,则∠E的度数为
如图,AD、BC相交于点F,AE、CE分别平分∠BAD、∠DCB,若∠B=25°,∠D=35°,则∠E的度数为 如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有( )
如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有( )