题目内容
19. 如图,在△ABC中,AB=AC=BC=8,点D为AB中点,点P从B点沿射线BC以2个单位/每秒运动,点Q从点C沿线段CA以1个单位/每秒运动,运动时间为t秒.求:
如图,在△ABC中,AB=AC=BC=8,点D为AB中点,点P从B点沿射线BC以2个单位/每秒运动,点Q从点C沿线段CA以1个单位/每秒运动,运动时间为t秒.求:(1)t为何值时,△BPD为直角三角形?
(2)t为何值时,△PCQ为等腰三角形?
(3)是否存在这样时刻t,使得△BPD与△PCQ全等?若存在,求出这样的时间t的值,若不存在,请说明理由.
分析 (1)分∠BPD=90°、∠BDP=90°两种情况,根据直角三角形的性质计算;
(2)根据等边三角形的性质和判定定理列出方程,解方程即可;
(3)分PC=BD、BD=CQ两种情况,根据全等三角形的判定定理进行判断即可.
解答 解:(1)当∠BPD=90°时,BP=$\frac{1}{2}$BD,即2×2t=4,
解得,t=1;
当∠BDP=90°时,
∵点D为AB中点,
∴点P与点C重合,
∴t=4;
∴当t=1或t=4时,△BPD为直角三角形;
(2)∵AB=AC=BC=8,
∴△ABC是等边三角形,
∴∠C=60°,
当△PCQ为等腰三角形时,△PCQ为等边三角形,
∴CP=CQ,即8-2t=t,
解得,t=$\frac{8}{3}$;
(3)不存在这样时刻t,使得△BPD与△PCQ全等.
当PC=BD时,8-2t=4,
解得,t=2,
则BP=4,
此时CQ=2,
∴BP≠CQ;
当BD=CQ时,t=4,
此时BP≠CP,
∴不存在这样时刻t,使得△BPD与△PCQ全等.
点评 本题考查的是等边三角形的性质、直角三角形的判定、等腰三角形的判定以及全等三角形的判定,掌握相关的性质定理和判定定理是解题的关键,解答时,注意分情况讨论思想的灵活运用.

练习册系列答案
相关题目
9. 如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则$\frac{OC}{CD}$的值为( )
如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则$\frac{OC}{CD}$的值为( )
 如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则$\frac{OC}{CD}$的值为( )
如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则$\frac{OC}{CD}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
10.用科学记数法表示0.009987,并保留两个有效数字是( )
| A. | 9.9×10-3 | B. | 1×10-2 | C. | 1.0×10-2 | D. | 0.10×10-3 |
 如图,正方形ABCD边长为1,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CE于点F,则EF的长为2$\sqrt{2}$.
如图,正方形ABCD边长为1,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CE于点F,则EF的长为2$\sqrt{2}$.

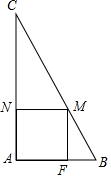 如图,在Rt△ABC中,∠A=90°,AB=2cm,AC=4cm.
如图,在Rt△ABC中,∠A=90°,AB=2cm,AC=4cm. 如图,某数学兴趣小组将周长为12的正方形铁丝框变形为一个扇形框,则所得扇形的面积的最大值为9.
如图,某数学兴趣小组将周长为12的正方形铁丝框变形为一个扇形框,则所得扇形的面积的最大值为9.