题目内容
7. 如图,正方形ABCD边长为1,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CE于点F,则EF的长为2$\sqrt{2}$.
如图,正方形ABCD边长为1,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CE于点F,则EF的长为2$\sqrt{2}$.
分析 根据角平分线的定义可得∠CAE=∠DAE,根据两直线平行,内错角相等可得∠E=∠DAE,从而得到∠E=∠CAE,再根据等角对等边可得AC=CE,根据等角的余角相等求出∠F=∠CAF,然后根据等角对等边可得AC=CF,最后求出EF=2AC,再根据正方形的对角线等于边长的$\sqrt{2}$倍求解即可.
解答 解:∵AE平分∠CAD,
∴∠CAE=∠DAE,
∵正方形对边AD∥BC,
∴∠E=∠DAE,
∴∠E=∠CAE,
∴AC=CE,
∵FA⊥AE,
∴∠E+∠F=90°,
∠CAE+∠CAF=90°,
∴∠F=∠CAF,
∴AC=CF,
∴EF=CF+CE=2AC,
∵正方形ABCD边长为1,
∴AC=$\sqrt{2}$,
∴EF=2AC=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查了正方形的性质,平行线的性质,等角的余角相等的性质,熟记各性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
17. 如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( )
如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( )
 如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( )
如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( )| A. | 60° | B. | 55° | C. | 50° | D. | 45° |
18.如果(2,5)表示电影票上的“2排5号”,那么“5排2号”应该表示为( )
| A. | (2,5) | B. | (5,2) | C. | (-5,-2) | D. | (-2,-5) |
16. 如图,沿对角线AC折叠正方形ABCD,使得B、D重合,再折叠△ACD,点D恰好落在AC上的点E处,测得折痕AF的长为3,则C到AF的距离CG为( )
如图,沿对角线AC折叠正方形ABCD,使得B、D重合,再折叠△ACD,点D恰好落在AC上的点E处,测得折痕AF的长为3,则C到AF的距离CG为( )
 如图,沿对角线AC折叠正方形ABCD,使得B、D重合,再折叠△ACD,点D恰好落在AC上的点E处,测得折痕AF的长为3,则C到AF的距离CG为( )
如图,沿对角线AC折叠正方形ABCD,使得B、D重合,再折叠△ACD,点D恰好落在AC上的点E处,测得折痕AF的长为3,则C到AF的距离CG为( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$-1 |
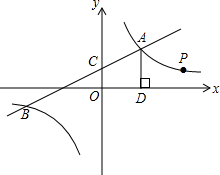 如图,一次函数y1=k1x+4与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于点A(2,m)和B(-6,-2)与y轴交于点C.
如图,一次函数y1=k1x+4与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于点A(2,m)和B(-6,-2)与y轴交于点C. 如图,在△ABC中,AB=AC=BC=8,点D为AB中点,点P从B点沿射线BC以2个单位/每秒运动,点Q从点C沿线段CA以1个单位/每秒运动,运动时间为t秒.求:
如图,在△ABC中,AB=AC=BC=8,点D为AB中点,点P从B点沿射线BC以2个单位/每秒运动,点Q从点C沿线段CA以1个单位/每秒运动,运动时间为t秒.求: