题目内容
 如图,直线y=-
如图,直线y=-| 3 |
| 4 |
| 5 |
| 4 |
(1)求点C的坐标;
(2)当0<t<5时,求S与t之间的函数关系式,并求S的最大值;
(3)当t>0时,直接写出点(4,
| 9 |
| 2 |
考点:一次函数综合题
专题:
分析:(1)简单求两直线的交点,建立二元一次方程组,得点C的坐标;
(2)根据几何关系把s用t表示,注意当MN在AD上时,这一特殊情况,转化为求函数最值问题;
(3)求定点在正方形PQMN内部时,t的范围,点E在x轴上运动,要用到分类讨论.
(2)根据几何关系把s用t表示,注意当MN在AD上时,这一特殊情况,转化为求函数最值问题;
(3)求定点在正方形PQMN内部时,t的范围,点E在x轴上运动,要用到分类讨论.
解答:解:(1)解方程
解得:
所以点C的坐标(3,
);
(2)直线y=-
x+6与x轴交于A点,
令0=-
x+6,
解得x=8,
∴A点的坐标为(8,0),
∵AE=t,
∴OE=8-t,
∴在直线y=-
x+6上,
当x=8-t时,y=-
(8-t)+6,
所以P(8-t,
t),Q(8-t,10-
t)在直线y=
x上,
当x=8-t时,
PQ=10-
t-
t=10-2t,
所以当0<t<5时,S与t之间的函数关系式为S=(10-2t)t,
即S=-2t2+10t;
二次函数y=ax2+bx+c图象的顶点坐标
当t=-t=-
=
时,S=
=
,
所以S的最大值是S=
;
(3)当t=5时,PQ=0,P,Q,C三点重合;
当t<5时,知OE=4时是临界条件,即8-t=4
即t=4
∴点Q的纵坐标为5>
,
点(4,
)在正方形边界PQ上,E继续往左移动,则点(4,
)进入正方形内部,但点Q的纵坐标再减少,当Q点的纵坐标为
时,OE=
∴8-t=
即t=
,
此时OE+PN=
+(10-2t)=
>4满足条件,
∴4<t<
,
当t>5时,由图和条件知,则有E(t-8,0),PQ=2t-10要满足点(4,
)在正方形的内部,
则临界条件N点横坐标为4?4=PQ+OE=|2t-10|+|t-8|=3t-18
即t=6,此时Q点的纵坐标为:-
×2+6=
.满足条件,
∴t>6.
综上所述:4<t<
或t>6.
|
解得:
|
所以点C的坐标(3,
| 15 |
| 4 |
(2)直线y=-
| 3 |
| 4 |
令0=-
| 3 |
| 4 |
解得x=8,
∴A点的坐标为(8,0),
∵AE=t,
∴OE=8-t,
∴在直线y=-
| 3 |
| 4 |
当x=8-t时,y=-
| 3 |
| 4 |
所以P(8-t,
| 3 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
当x=8-t时,
PQ=10-
| 5 |
| 4 |
| 3 |
| 4 |
所以当0<t<5时,S与t之间的函数关系式为S=(10-2t)t,
即S=-2t2+10t;
二次函数y=ax2+bx+c图象的顶点坐标
当t=-t=-
| b |
| 2a |
| 5 |
| 2 |
| 4ac-b2 |
| 4a |
| 25 |
| 2 |
所以S的最大值是S=
| 25 |
| 2 |
(3)当t=5时,PQ=0,P,Q,C三点重合;

当t<5时,知OE=4时是临界条件,即8-t=4
即t=4
∴点Q的纵坐标为5>
| 9 |
| 2 |
点(4,
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 18 |
| 5 |
∴8-t=
| 18 |
| 5 |
| 22 |
| 5 |
此时OE+PN=
| 18 |
| 5 |
| 24 |
| 5 |
∴4<t<
| 22 |
| 5 |
当t>5时,由图和条件知,则有E(t-8,0),PQ=2t-10要满足点(4,
| 9 |
| 2 |
则临界条件N点横坐标为4?4=PQ+OE=|2t-10|+|t-8|=3t-18
即t=6,此时Q点的纵坐标为:-
| 3 |
| 4 |
| 9 |
| 2 |
∴t>6.
综上所述:4<t<
| 22 |
| 5 |
点评:此题考查函数基本性质,求函数最值问题,第三问考查动点问题,求t的范围,观察图形,搞清几何坐标,理清思路,又运用分类讨论思想.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
下列各点中,在第一象限的点是( )
| A、(4,3) |
| B、(2,-3) |
| C、(-2,3) |
| D、(-2,-3) |
 如图,已知抛物线y=x2+bx+c与x轴交于点A(-1,0)、C,与y轴交于点B(0,3),抛物线的顶点为P.
如图,已知抛物线y=x2+bx+c与x轴交于点A(-1,0)、C,与y轴交于点B(0,3),抛物线的顶点为P.

 如图,在平面直角坐标系中,抛物线
如图,在平面直角坐标系中,抛物线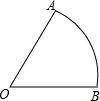 如图,扇形OAB的圆心角为2α,点P为弧AB上一点,将此扇形翻折,当点O和点P重合时折痕恰巧过点B,且
如图,扇形OAB的圆心角为2α,点P为弧AB上一点,将此扇形翻折,当点O和点P重合时折痕恰巧过点B,且 为了解某学校八年级学生的身体发育情况,学校对八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)
为了解某学校八年级学生的身体发育情况,学校对八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)