题目内容
4.已知二次函数y=3x2+c与正比例函数y=4x的图象只有一个交点,则c的值为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | 3 | D. | 4 |
分析 由$\left\{\begin{array}{l}{y=3{x}^{2}+c}\\{y=4x}\end{array}\right.$,消去y得到3x2-4x+c=0,因为二次函数y=3x2+c与正比例函数y=4x的图象只有一个交点,所以△=0,列出方程即可解决问题.
解答 解:由$\left\{\begin{array}{l}{y=3{x}^{2}+c}\\{y=4x}\end{array}\right.$,
消去y得到3x2-4x+c=0,
∵二次函数y=3x2+c与正比例函数y=4x的图象只有一个交点,
∴△=0,
∴16-12c=0,
∴c=$\frac{4}{3}$.
故选A
点评 本题考查二次函数性质,二元二次方程组,根的判别式等知识,解题的关键是学会元转化 的思想思考问题,所以中考常考题型.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
12.下列说法错误的是( )
| A. | 投掷一枚均匀的骰子,朝上一面的点数是3的概率是$\frac{1}{3}$ | |
| B. | 不可能事件发生的概率为0 | |
| C. | 买一张彩票中奖是随机事件 | |
| D. | 一个事件发生的概率为1%,这件事件就有可能发生 |
13.一个长方形的周长为6a+8b,其中一边长为2a-b,则另一边长为( )
| A. | 4a+5b | B. | a+b | C. | a+5b | D. | a+7b |
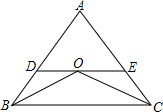 如图,已知OB、OC为△ABC的角平分线,DE∥BC,△ADE的周长为10,BC长为8,求△ABC的周长.
如图,已知OB、OC为△ABC的角平分线,DE∥BC,△ADE的周长为10,BC长为8,求△ABC的周长.
 有两棵树,一棵高5米,另一棵高2米,两棵树的距离有4米,一只小鸟从一棵树的树顶端飞到另一棵树的顶端,那么请问:这只小鸟至少要飞了5米.
有两棵树,一棵高5米,另一棵高2米,两棵树的距离有4米,一只小鸟从一棵树的树顶端飞到另一棵树的顶端,那么请问:这只小鸟至少要飞了5米.