题目内容
16. 如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,8),点D是OA的中点,点P在BC边上以每秒1个单位长度的速度由点C向点B运动.
如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,8),点D是OA的中点,点P在BC边上以每秒1个单位长度的速度由点C向点B运动.(1)当t为何值时,四边形PODB是平行四边形?
(2)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(3)当△OPD为等腰三角形时,写出点P的坐标(不必写过程).
分析 (1)由于PB∥OD,根据平行四边形的判定可知当PB=OD=10时,四边形PODB是平行四边形,再求出PC=10,从而求出t的值;
(2)根据菱形的判定,当OD=OP=PQ=10时,ODQP为菱形,在Rt△OPC中,利用勾股定理求出CP的值,进而求出t的值及Q点的坐标;
(3)当△OPD为等腰三角形时,分三种情况进行讨论:①如果O为顶点,那么OP=OD=10;②如果P为顶点,那么PO=PD;③如果D为顶点,那么DP=DO=10.
解答 解:(1)∵A(20,0),C(0,8),
∴OA=20,OC=8,
∵点D是OA的中点,
∴OD=$\frac{1}{2}$OA=10,
∵四边形OABC为矩形,
∴BC=OA=20,
∵四边形PODB是平行四边形,
∴PB=OD=10,
∴PC=BC-PB=10,
∴t=10; (2)如图1,∵四边形ODQP为菱形,
(2)如图1,∵四边形ODQP为菱形,
∴OD=OP=PQ=10,
∴在Rt△OPC中,由勾股定理得:PC=$\sqrt{O{P}^{2}-O{C}^{2}}$=6,
∴t=6,
∴CQ=CP+PQ=6+10=16,
∴Q点的坐标为(16,8);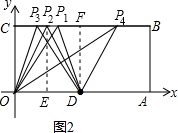 (3)如图2,△OPD为等腰三角形时,分三种情况:
(3)如图2,△OPD为等腰三角形时,分三种情况:
①如果O为顶点,那么OP=OD=10,
由勾股定理可以求得PC=6,此时P1(6,8);
②如果P为顶点,那么PO=PD,
作PE⊥OA于E,则OE=ED=5,此时P2(5,8);
③如果D为顶点,那么DP=DO=10,
作DF⊥BC于F,由勾股定理,得PF=6,
∴P3C=10-6=4或P4C=10+6=16,此时P3(4,8),P4(16,8).
综上所述,满足条件的点P的坐标为P1(6,8),P2(5,8),P3(4,8),P4(16,8).
点评 此题属于四边形综合题.考查了矩形的性质,坐标与图形的性质,等腰三角形的性质,平行四边形的判定及性质,菱形的判定及性质以及勾股定理的运用.注意利用数形结合、分类讨论思想求解是解题的关键.

 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 如图,已知直线AB是线段CD的垂直平分线,下列说法正确的是( )
如图,已知直线AB是线段CD的垂直平分线,下列说法正确的是( )| A. | AC=BC | B. | AD=BD | C. | BC=BD | D. | AB=CD |
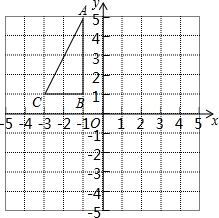 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,5),B(-1,1),C(-3,1).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,5),B(-1,1),C(-3,1).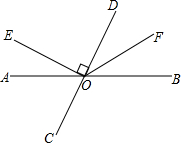 如图,直线AB、CD相交于点O,OE⊥CD,OF平分∠BOD.
如图,直线AB、CD相交于点O,OE⊥CD,OF平分∠BOD. 如图,在平面直角坐标系中,点B是反比例函数y=$\frac{k}{x}$的图象上任意一点,将点B绕原点O顺时针方向旋转90°到点A.
如图,在平面直角坐标系中,点B是反比例函数y=$\frac{k}{x}$的图象上任意一点,将点B绕原点O顺时针方向旋转90°到点A.