题目内容
14.以下列各组数为三角形的边长,能构成直角三角形的是( )| A. | 2、3、4 | B. | 5、5、6 | C. | 2、$\sqrt{3}$、$\sqrt{5}$ | D. | $\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$ |
分析 根据勾股定理的逆定理得出选项A、B、C不能构成直角三角形,D选项能构成直角三角形,即可得出结论.
解答 解:A、22+32≠42,不符合勾股定理的逆定理,故不正确;
B、52+52≠62,不符合勾股定理的逆定理,故不正确;
C、22+($\sqrt{3}$)2≠($\sqrt{5}$)2,不符合勾股定理的逆定理,故不正确;
D、($\sqrt{2}$)2+($\sqrt{3}$)2=($\sqrt{5}$)2,符合勾股定理的逆定理,能构成直角三角形,故正确.
故选:D.
点评 本题考查了勾股定理的逆定理;在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列说法正确的是( )
| A. | a2b的系数为1,次数为2 | B. | -xy的系数为1,次数为2 | ||
| C. | πx的系数为1,次数为2 | D. | -5xy2的系数为-5,次数为3 |
5.若把分式$\frac{x+y}{2xy}$中的x和y都扩大3倍,那么分式的值为原来的( )
| A. | 3倍 | B. | 不变 | C. | $\frac{1}{3}$ | D. | 6倍 |
6.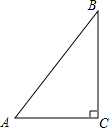 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
 如图,△ABC中,AB=AC,BD⊥AC,BD=6,E为AB边的中点,ED=5,则DC=2.
如图,△ABC中,AB=AC,BD⊥AC,BD=6,E为AB边的中点,ED=5,则DC=2. 如图,四边形OABC为菱形,点B、C在以点O为圆心的$\widehat{EF}$上,若OA=1cm,∠1=∠2,则$\widehat{EF}$的长为$\frac{2π}{3}$cm.
如图,四边形OABC为菱形,点B、C在以点O为圆心的$\widehat{EF}$上,若OA=1cm,∠1=∠2,则$\widehat{EF}$的长为$\frac{2π}{3}$cm. 已知:如图,AB是⊙O的直径,AB=6,点C,D在⊙O上,且CD平分∠ACB,∠CAB=60°.
已知:如图,AB是⊙O的直径,AB=6,点C,D在⊙O上,且CD平分∠ACB,∠CAB=60°.