题目内容
6.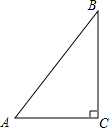 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
分析 根据勾股定理,可得AB的长,根据锐角的余弦等于邻边比斜边,可得答案.
解答 解:在Rt△ABC中,∠C=90°,AC=3,BC=4,
由勾股定理,得
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5.
cosA=$\frac{AC}{AB}$=$\frac{3}{5}$,
故选:A.
点评 本题考查了锐角三角函数的定义,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
16.解方程2x-(x+10)=5x+2(x-1)得到2x-x-10=5x+2x-2的步骤是( )
| A. | 去括号 | B. | 移项 | C. | 合并同类项 | D. | 系数化为1 |
14.以下列各组数为三角形的边长,能构成直角三角形的是( )
| A. | 2、3、4 | B. | 5、5、6 | C. | 2、$\sqrt{3}$、$\sqrt{5}$ | D. | $\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$ |
15.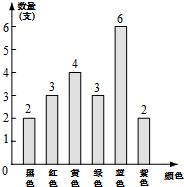 有一盒水彩笔除了颜色外无其他差别,其中各种颜色的数量统计如图所示.小腾在无法看到盒中水彩笔颜色的情形下随意抽出一支.小腾抽到蓝色水彩笔的概率为( )
有一盒水彩笔除了颜色外无其他差别,其中各种颜色的数量统计如图所示.小腾在无法看到盒中水彩笔颜色的情形下随意抽出一支.小腾抽到蓝色水彩笔的概率为( )
 有一盒水彩笔除了颜色外无其他差别,其中各种颜色的数量统计如图所示.小腾在无法看到盒中水彩笔颜色的情形下随意抽出一支.小腾抽到蓝色水彩笔的概率为( )
有一盒水彩笔除了颜色外无其他差别,其中各种颜色的数量统计如图所示.小腾在无法看到盒中水彩笔颜色的情形下随意抽出一支.小腾抽到蓝色水彩笔的概率为( )| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{20}$ |
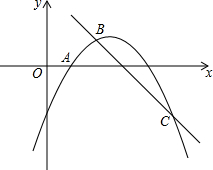 如图,在平面直角坐标系xOy中,二次函数y=-$\frac{1}{2}{x^2}$+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=-x+3与二次函数y=-$\frac{1}{2}{x^2}$+bx+c的图象分别交于B,C两点,点B在第一象限.
如图,在平面直角坐标系xOy中,二次函数y=-$\frac{1}{2}{x^2}$+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=-x+3与二次函数y=-$\frac{1}{2}{x^2}$+bx+c的图象分别交于B,C两点,点B在第一象限.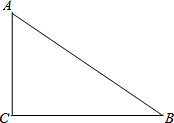 如图,已知△ABC,∠C=90°,AC<BC,若D为BC上一点,且到A,B两点距离相等.
如图,已知△ABC,∠C=90°,AC<BC,若D为BC上一点,且到A,B两点距离相等.