题目内容
3.已知扇形的面积为15πcm2,半径长为5cm,则扇形周长为6π+10cm.分析 根据扇形的面积公式求出扇形弧长,根据扇形周长公式计算即可.
解答 解:由扇形的面积公式S=$\frac{1}{2}$lr,得,
l=$\frac{2S}{r}$=6πcm,
则扇形周长=(6π+10)cm,
故答案为:6π+10.
点评 本题考查的是扇形的面积的计算,掌握S扇形=$\frac{1}{2}$lR(其中l为扇形的弧长)是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列几种说法中,不正确的( )
| A. | 任意有理数a的相反数是-a | |
| B. | 在一个数前面加上“-”号所得的数是负数 | |
| C. | 一个非0有理数a的倒数是$\frac{1}{a}$ | |
| D. | 最小的自然数是0 |
14.以下列各组数为三角形的边长,能构成直角三角形的是( )
| A. | 2、3、4 | B. | 5、5、6 | C. | 2、$\sqrt{3}$、$\sqrt{5}$ | D. | $\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$ |
15.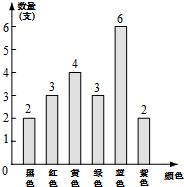 有一盒水彩笔除了颜色外无其他差别,其中各种颜色的数量统计如图所示.小腾在无法看到盒中水彩笔颜色的情形下随意抽出一支.小腾抽到蓝色水彩笔的概率为( )
有一盒水彩笔除了颜色外无其他差别,其中各种颜色的数量统计如图所示.小腾在无法看到盒中水彩笔颜色的情形下随意抽出一支.小腾抽到蓝色水彩笔的概率为( )
 有一盒水彩笔除了颜色外无其他差别,其中各种颜色的数量统计如图所示.小腾在无法看到盒中水彩笔颜色的情形下随意抽出一支.小腾抽到蓝色水彩笔的概率为( )
有一盒水彩笔除了颜色外无其他差别,其中各种颜色的数量统计如图所示.小腾在无法看到盒中水彩笔颜色的情形下随意抽出一支.小腾抽到蓝色水彩笔的概率为( )| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{20}$ |
12.下列方程有实数根的是( )
| A. | x2+10=0 | B. | x2+x+1=0 | C. | x2-x-1=0 | D. | x2-$\sqrt{2}$x+1=0 |
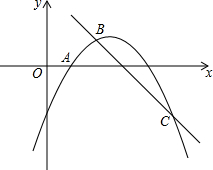 如图,在平面直角坐标系xOy中,二次函数y=-$\frac{1}{2}{x^2}$+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=-x+3与二次函数y=-$\frac{1}{2}{x^2}$+bx+c的图象分别交于B,C两点,点B在第一象限.
如图,在平面直角坐标系xOy中,二次函数y=-$\frac{1}{2}{x^2}$+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=-x+3与二次函数y=-$\frac{1}{2}{x^2}$+bx+c的图象分别交于B,C两点,点B在第一象限.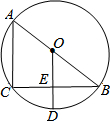 如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC.
如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC.