题目内容
6．已知|x+2y-1|+（2x-y-2）2=0，求（2x+y）2-2（2x-y）（2x+y）+（2x-y）2的值．分析 由已知等式，利用非负数的性质列出方程组，求出方程组的解得到x与y的值，原式利用完全平方公式化简，将x与y的值代入计算即可求出值．
解答 解：∵|x+2y-1|+（2x-y-2）2=0，
∴$\left\{\begin{array}{l}{x+2y=1}\\{2x-y=2}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$，
则原式=[（2x+y）-（2x-y）]2=（2y）2=4y2=0．
点评 此题考查了因式分解-运用公式法，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
14．填表：
| 单项式 | -$\frac{{a}^{2}{b}^{3}c}{2}$ | -0.5xyz2 | m | 0 | 3a2b |
| 系数 | -$\frac{1}{2}$ | -0.5 | 1 | 0 | 3 |
| 次数 | 6 | 4 | 1 | 0 | 3 |
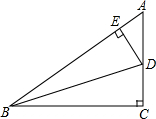在Rt△ABC中，BD平分∠ABC，DE⊥AB于E；