��Ŀ����
14��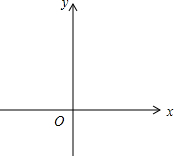 ��ͼ����ƽ��ֱ������ϵxOy�У����κ���y=$\frac{1}{3}{x^2}$+bx+c��ͼ����y�ύ�ڵ�A����˫����y=$\frac{8}{x}$��һ��������B�����ĺ�����Ϊ4������B��ֱ��l��x�ᣬ��ö��κ���ͼ������һ����C��ֱ��AC��y���ϵĽؾ���-6��
��ͼ����ƽ��ֱ������ϵxOy�У����κ���y=$\frac{1}{3}{x^2}$+bx+c��ͼ����y�ύ�ڵ�A����˫����y=$\frac{8}{x}$��һ��������B�����ĺ�����Ϊ4������B��ֱ��l��x�ᣬ��ö��κ���ͼ������һ����C��ֱ��AC��y���ϵĽؾ���-6����1������κ����Ľ���ʽ��
��2����ֱ��AC�ı���ʽ��
��3��ƽ�����Ƿ���ڵ�D��ʹA��B��C��DΪ������ı����ǵ������Σ�������ڣ������D���ꣻ��������ڣ�˵�����ɣ�
���� ��1������õ�A���B�����꣬Ȼ�����ݴ���ϵ��������������ߵĽ���ʽ��
��2������������ߵĶԳ���Ϊx=-1�����ݵ�B���C����x=-1�Գƣ�����õ�C�����꣬Ȼ�����ݴ���ϵ���������ֱ��AC�Ľ���ʽ��
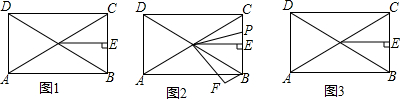
��3���ٵ�CD��ABʱ��AC=BC���ʵ�D�����ڣ�����ͼ1��ʾ����AD��BCʱ��AB��AC������A��BCƽ����l����CΪԲ�ģ�ABΪ�뾶��������l���D1�㣬���ݵ�A��D1����x=-1�Գƿ���õ�D1�����ꣻ����ͼ2��ʾ��BD��ACʱ������C��CM��x�ᣬ����A��AM��y�ᣬ����B��BF��AC��D2E��AC��������AAS֤����AMC�ա�CBF���Ӷ������AF=CE=4�����ǵõ�D2B=2��Ȼ����֤��BHD2�ס�AMC���Ӷ������BH=$\frac{6}{5}$��HD2=$\frac{8}{5}$�����ǿ���õ�D2�����꣮
��� �⣺��1���߽�x=4����y=$\frac{8}{x}$�ã�y=2��
��B��4��2����
�ߵ�A��y���ϣ���ֱ��AC��y���ϵĽؾ���-6��
��A��0��-6����
�߽�B��4��2����A��0��-6�����������ߵĽ���ʽ�ã�$\left\{\begin{array}{l}{c=-6}\\{\frac{16}{3}+4b+c=2}\end{array}\right.$����ã�$\left\{\begin{array}{l}{b=\frac{2}{3}}\\{c=-6}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{1}{3}{x}^{2}$+$\frac{2}{3}x$-6��
��2���������ߵĶԳ���Ϊx=-$\frac{b}{2a}=-\frac{\frac{2}{3}}{\frac{1}{3}��2}$=-1��
���B����x=-1�ĶԳƵ�C������Ϊ��-6��2����
��ֱ��AC�Ľ���ʽΪy=kx+b��
�߽���A��0��-6����C��-6��2������ã�$\left\{\begin{array}{l}{b=-6}\\{-6k+b=2}\end{array}\right.$����ã�k=-$\frac{4}{3}$��b=-6��
��ֱ��AC�Ľ���ʽΪy=$-\frac{4}{3}x$-6��
��3���١�B��4��2��C��-6��2����
��BC=10��
��A��0��-6����C��-6��2����
��AC=$\sqrt{{6}^{2}+{8}^{2}}$=10��
��AC=BC��
�൱CD��ABʱ�������ڵ�Dʹ���ı���A��B��C��DΪ������ı����ǵ������Σ�
����ͼ1��ʾ��
��AD��BCʱ��AB��AC������A��BCƽ����l����CΪԲ�ģ�ABΪ�뾶��������l���D1�㣬A��D1����x=-1�Գƣ�
��D1��-2��-6����
����ͼ2��ʾ��BD��ACʱ������C��CM��x�ᣬ����A��AM��y�ᣬ����B��BF��AC��D2E��AC��
��CB��AM��
���BCA=��CAM��
�ڡ�AMC�͡�CBF�У�
$\left\{\begin{array}{l}{��BCA=��CAM}\\{��AMC=��BFC=90��}\\{AC=BC}\end{array}\right.$��
���AMC�ա�CBF��
��CF=AM=6��
��AF=4��
������ABD2C�ǵ������Σ�
��CE=AF=4��
��D2B=EF=2��
��BD2��AC��
���D2BH=��BCA��
�ߡ�BCA=��CAM��
���D2BH=��CAM��
�֡ߡ�M=��D2HB��
��BHD2�ס�AMC��
��$\frac{{D}_{2}H}{HB}=\frac{4}{3}$��
��BD2=2��
��BH=$\frac{6}{5}$��HD2=$\frac{8}{5}$��
��D2��$\frac{14}{5}$��$\frac{18}{5}$����
������������D��������-2��-6����D2��$\frac{14}{5}$��$\frac{18}{5}$����
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ������һ�κ��������κ����Ľ���ʽ��ȫ�������ε����ʺ��ж������������ε����ʺ��ж����������ε����ʣ����BD2=2�ǽ���Ĺؼ���

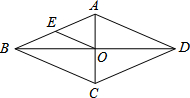 ������ABCD�У�EΪAB���е㣬OE=3��������ABCD���ܳ�Ϊ24��
������ABCD�У�EΪAB���е㣬OE=3��������ABCD���ܳ�Ϊ24�� ��k��0��������y1=��x-k��2+2k��y2=-��x+k��2-2k��ͼ����y�����ν���A��B���㣬����y1��y2��ͼ��Ķ���ֱ�ΪC��D��
��k��0��������y1=��x-k��2+2k��y2=-��x+k��2-2k��ͼ����y�����ν���A��B���㣬����y1��y2��ͼ��Ķ���ֱ�ΪC��D�� ��ͼ��Ҫʹ��Ϊ2�ľ���ƽ�峵ABCDͨ����Ϊ2$\sqrt{2}$�ĵȿ���ֱ��ͨ����ƽ�峵�ij����ܳ���4�ף�
��ͼ��Ҫʹ��Ϊ2�ľ���ƽ�峵ABCDͨ����Ϊ2$\sqrt{2}$�ĵȿ���ֱ��ͨ����ƽ�峵�ij����ܳ���4�ף� ijͬѧ�ھ������BC����ˮƽ����200��A����������C������Ϊ20�㣨�������������أ��������BC�ĸ�ԼΪ��������
ijͬѧ�ھ������BC����ˮƽ����200��A����������C������Ϊ20�㣨�������������أ��������BC�ĸ�ԼΪ�������� ��Բ�桢ֱ����ͼ����д��������Ҫ������ͼ�ۼ���
��Բ�桢ֱ����ͼ����д��������Ҫ������ͼ�ۼ���