题目内容
16.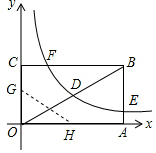 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(8,n)在边AB上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=$\frac{1}{2}$.
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(8,n)在边AB上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=$\frac{1}{2}$.(1)求反比例函数的解析式和n的值;
(2)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求G点的坐标.
分析 (1)在Rt△BOA中,由OA=8,推出AB=OA×tan∠BOA=4,由点D为OB的中点,点B(8,4),可得点D(4,2),n=4,又,点D在y=$\frac{k}{x}$的图象上,可得k=8;
(2)设点F(a,4),推出4a=8,推出CF=a=2,连结FG,设OG=t,则OG=FG=t CG=4-t,Rt△CGF中,根据GF2=CF2+CG2,可得,t2=(4-t)2+12,解方程即可;
解答 解:(1)在Rt△BOA中,∵OA=8,
∴AB=OA×tan∠BOA=4,
∴n=4
∵点D为OB的中点,点B(8,4),
∴点D(4,2),
又∵点D在y=$\frac{k}{x}$的图象上,
∴2=$\frac{k}{4}$,
∴k=8,
∴y=$\frac{8}{x}$.
(2)设点F(a,4),
∴4a=8,
∴CF=a=2,
连结FG,设OG=t,则OG=FG=t CG=4-t,
Rt△CGF中,GF2=CF2+CG2,
∴t2=(4-t)2+12,
∴t=2.5,
∴G点的坐标为(0,2.5).
点评 本题考查反比例函数的性质、矩形的性质、待定系数法、锐角三角函数、勾股定理等知识,解题的关键是学会利用参数,构建方程解决问题,属于中考常考题型.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
6.下列运算正确的是( )
| A. | x3+x2=x5 | B. | x3•x2=x6 | C. | (x3)2=x9 | D. | x3÷x2=x |
7.某校九年级体育模拟测试中,六名男生引体向上的成绩如下(单位:个):10、6、9、11、8、10,下列关于这组数据描述正确的是( )
| A. | 中位数是10 | B. | 众数是10 | C. | 平均数是9.5 | D. | 方差是16 |
4.下列调查中,最适合采用全面调查(普查)的是( )
| A. | 对某区中小学生的睡眠时间的调查 | |
| B. | 对我市初中学生的兴趣爱好的调查 | |
| C. | 对我市中学教师的健康状况的调查 | |
| D. | 对“天宫二号”飞行器各零部件的质量的调查 |
11.下列图案中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.下列四个命题中,属于真命题的共有( )
①相等的圆心角所对的弧相等 ②若$\sqrt{ab}$=$\sqrt{a}$•$\sqrt{b}$,则a、b都是非负实数
③相似的两个图形一定是位似图形 ④三角形的内心到这个三角形三边的距离相等.
①相等的圆心角所对的弧相等 ②若$\sqrt{ab}$=$\sqrt{a}$•$\sqrt{b}$,则a、b都是非负实数
③相似的两个图形一定是位似图形 ④三角形的内心到这个三角形三边的距离相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.已知a,b,c∈R,a<0且b>0,则下列不等式中一定成立的是( )
| A. | a2<b2 | B. | ac2>bc2 | C. | $\frac{1}{|a|}$>$\frac{1}{b}$ | D. | $\frac{1}{a-b}$>$\frac{1}{a}$ |
 在“校园读书月”活动中,小华调查了班级里40名同学本学期购买课外书的花费情况,并将结果绘制成如图所示的统计图.下面有四个推断:
在“校园读书月”活动中,小华调查了班级里40名同学本学期购买课外书的花费情况,并将结果绘制成如图所示的统计图.下面有四个推断: