��Ŀ����
��ͼ���ı���AOBC�������Σ���C�������ǣ�4
��0��������P�ӵ�O��������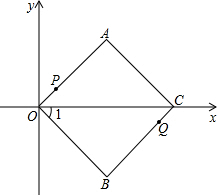 ����OACB���������˶�����һ����Q�ӵ�C������������CBOA���������˶���
����OACB���������˶�����һ����Q�ӵ�C������������CBOA���������˶���
��1�����A��������������AOBC�������
��2�����������Ƶ�O˳ʱ����ת45�㣬����ת�����������ԭ�����ε��ص����ֵ������
��3����P���˶��ٶ���1����λ/ÿ�룬Q���˶��ٶ���2����λ/ÿ�룬P��Q����ͬʱ��������Q�˶�����A ʱP��Qͬʱֹͣ�˶������˶�ʱ��Ϊt�룬�Ƿ����������tֵ��ʹ��OPQ��Ϊ���������Σ������ڣ������Q������ꣻ�������ڣ���˵�����ɣ�
| 2 |
 ����OACB���������˶�����һ����Q�ӵ�C������������CBOA���������˶���
����OACB���������˶�����һ����Q�ӵ�C������������CBOA���������˶�����1�����A��������������AOBC�������
��2�����������Ƶ�O˳ʱ����ת45�㣬����ת�����������ԭ�����ε��ص����ֵ������
��3����P���˶��ٶ���1����λ/ÿ�룬Q���˶��ٶ���2����λ/ÿ�룬P��Q����ͬʱ��������Q�˶�����A ʱP��Qͬʱֹͣ�˶������˶�ʱ��Ϊt�룬�Ƿ����������tֵ��ʹ��OPQ��Ϊ���������Σ������ڣ������Q������ꣻ�������ڣ���˵�����ɣ�
��������1������AB�����ݡ�OCAΪ���������οɵ�AD=OD�ij����Ӷ��ó���A�����꣬��ó�������AOBC�������
��2��������ת�����ʿɵ�OA��ij����Ӷ��ó�A��C��A��E�������������ɣ�
��3�����ڣ���Q���ڲ�ͬ���߶����˶�������ɷ�Ϊ���֣�
�ٵ�Q����BC��ʱ��ʹOQ=QP������OP=2BQ����OP=t��BQ=4-2t����ʽ�ɵó�t��
�ڵ�Q����OB��ʱ��ʹOQ=OP����OP=t��OQ=8-2t����ʽ�ɵó�t��
�۵�Q����OA��ʱ��ʹOQ=PQ����ʽ�ɵó�t��
��2��������ת�����ʿɵ�OA��ij����Ӷ��ó�A��C��A��E�������������ɣ�
��3�����ڣ���Q���ڲ�ͬ���߶����˶�������ɷ�Ϊ���֣�
�ٵ�Q����BC��ʱ��ʹOQ=QP������OP=2BQ����OP=t��BQ=4-2t����ʽ�ɵó�t��
�ڵ�Q����OB��ʱ��ʹOQ=OP����OP=t��OQ=8-2t����ʽ�ɵó�t��
�۵�Q����OA��ʱ��ʹOQ=PQ����ʽ�ɵó�t��
��� �⣺��1������AB����OC���ڵ�D��
�⣺��1������AB����OC���ڵ�D��
�ɡ�OCAΪ����Rt������AD=OD=
OC=2
����1�֣�
���A��������2
��2
������2�֣�
������AOBC�����16��1�֣�
��2����ת��ɵ�OA��=OB=4����1�֣�
��A��C=4
-4������֪��CA��E=90�㣬��OCB=45�㣬
���A��EC�ǵ���ֱ�������Σ�
��A��E=A��C=4
-4����1�֣�
��S�ı���OA��EB=S��OBC-S��A��EC=16
-16����2�֣�
��3�����ڣ���Q���ڲ�ͬ���߶����˶�������ɷ�Ϊ���֣�
�ٵ�Q����BC��ʱ��ʹOQ=QP��QMΪOP�Ĵ�ֱƽ���ߣ�
����OP=2OM=2BQ����OP=t��BQ=4-2t��

��t=2��4-2t����
��t=
����1�֣�
��Q��
��-
��
�ڵ�Q����OB��ʱ��ʹOQ=OP����OP=t��OQ=8-2t��
��t=8-2t��
��t=
����1�֣�
��Q��
��-
��
�۵�Q����OA��ʱ��ʹOQ=PQ��t2-24t+96=0��t=12+4
����ȥ����t=12-4
����2�֣�
��Q��4
��4
��
��ע�������ֻⷨҪ��ȷ��ͬ����Ӧ���֣�
 �⣺��1������AB����OC���ڵ�D��
�⣺��1������AB����OC���ڵ�D���ɡ�OCAΪ����Rt������AD=OD=
| 1 |
| 2 |
| 2 |
���A��������2
| 2 |
| 2 |
������AOBC�����16��1�֣�
��2����ת��ɵ�OA��=OB=4����1�֣�
��A��C=4
| 2 |
���A��EC�ǵ���ֱ�������Σ�
��A��E=A��C=4
| 2 |
��S�ı���OA��EB=S��OBC-S��A��EC=16
| 2 |
��3�����ڣ���Q���ڲ�ͬ���߶����˶�������ɷ�Ϊ���֣�
�ٵ�Q����BC��ʱ��ʹOQ=QP��QMΪOP�Ĵ�ֱƽ���ߣ�
����OP=2OM=2BQ����OP=t��BQ=4-2t��

��t=2��4-2t����
��t=
| 8 |
| 5 |
��Q��
12
| ||
| 5 |
8
| ||
| 5 |
�ڵ�Q����OB��ʱ��ʹOQ=OP����OP=t��OQ=8-2t��
��t=8-2t��
��t=
| 8 |
| 3 |
��Q��
4
| ||
| 3 |
4
| ||
| 3 |
�۵�Q����OA��ʱ��ʹOQ=PQ��t2-24t+96=0��t=12+4
| 3 |
| 3 |
��Q��4
| 11 |
| 11 |
��ע�������ֻⷨҪ��ȷ��ͬ����Ӧ���֣�
������������һ���ۺ���Ŀ�������������ε����ʣ����������ε��ж��Լ���ת�����ʣ����п�ѹ���⣬�ۺ��Խ�ǿ���ѶȽϴ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
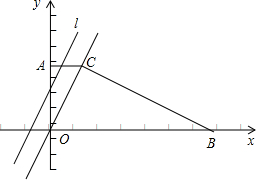 C��ֱ��lΪ��y=2x+t��l��A��ƽ�Ƶ�B��ʱ��l��ֱ������AOBC������Χ�ɵ������ε������ΪS��
C��ֱ��lΪ��y=2x+t��l��A��ƽ�Ƶ�B��ʱ��l��ֱ������AOBC������Χ�ɵ������ε������ΪS��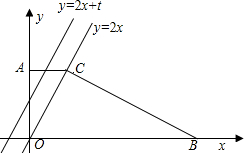 ʽΪy=2x��ƽ����OC��ֱ��m�Ľ���ʽΪy=2x+t��ֱ��m��A��ƽ�Ƶ�B��ʱ��m��ֱ������AOBC������Χ�ɵ������ε������ΪS��
ʽΪy=2x��ƽ����OC��ֱ��m�Ľ���ʽΪy=2x+t��ֱ��m��A��ƽ�Ƶ�B��ʱ��m��ֱ������AOBC������Χ�ɵ������ε������ΪS��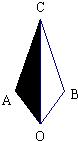 23����ͼ���ı���AOBC�У���AOB=72�㣬��ACB=36�㣬OA=OB��AC=BC����O���ģ���˳ʱ�뷽���ı���AOBC��ת72�㣬�뻭��������ת�Ĵε�ͼ�Σ�����Ӱ���֣�
23����ͼ���ı���AOBC�У���AOB=72�㣬��ACB=36�㣬OA=OB��AC=BC����O���ģ���˳ʱ�뷽���ı���AOBC��ת72�㣬�뻭��������ת�Ĵε�ͼ�Σ�����Ӱ���֣� �ƶ���ͬʱ����Q�ӵ�O��ʼ��ÿ��a��1��a��3������λ���ȵ��ٶ�������OB�����ƶ�����t��0��t��4�����PQ��OC�ڵ�R��
�ƶ���ͬʱ����Q�ӵ�O��ʼ��ÿ��a��1��a��3������λ���ȵ��ٶ�������OB�����ƶ�����t��0��t��4�����PQ��OC�ڵ�R�� ��ͼ���ı���AOBC�У�AC=BC����A+��OBC=180�㣬CD��OA��D��
��ͼ���ı���AOBC�У�AC=BC����A+��OBC=180�㣬CD��OA��D��