题目内容
19.?ABCD的对角线交于点O,下列结论错误的是( )| A. | △AOB≌△BOC | B. | △AOB≌△COD | ||
| C. | ?ABCD是中心对称图形 | D. | △AOB与△BOC的面积相等 |
分析 由平行四边形的性质得出OA=OC,OB=OD,得出△AOB的面积=△BOC的面积,平行四边形是中心对称图形,由SAS证出△AOB≌△COD;即可得出结论.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴△AOB的面积=△BOC的面积,平行四边形是中心对称图形,
在△AOB和△COD中,$\left\{\begin{array}{l}{OA=OC}&{\;}\\{∠AOB=∠COD}&{\;}\\{OB=OC}&{\;}\end{array}\right.$,
∴△AOB≌△COD(SAS),
∴B、C、D正确,A错误;
故选:A.
点评 本题考查了平行四边形的性质、全等三角形的判定、三角形的面积;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
9. 如图,点A、B、C均在⊙O上,∠C=50°,则∠OAB的大小是( )
如图,点A、B、C均在⊙O上,∠C=50°,则∠OAB的大小是( )
 如图,点A、B、C均在⊙O上,∠C=50°,则∠OAB的大小是( )
如图,点A、B、C均在⊙O上,∠C=50°,则∠OAB的大小是( )| A. | 50° | B. | 40° | C. | 25° | D. | 100° |
 如图,已知AD∥BC,∠B=32°,BD平分∠ADE,则∠DEC=64°.
如图,已知AD∥BC,∠B=32°,BD平分∠ADE,则∠DEC=64°. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则S10的值为235.
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则S10的值为235.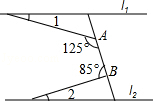 如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=30°.
如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=30°.