题目内容
5．已知不等式组$\left\{\begin{array}{l}{2x-a+b＜1}\\{x-2（b-2a）＞3}\end{array}\right.$的解集是-1＜x＜1，则a与b的值等于多少？分析 首先解不等式组求得不等式组，然后根据解集是-1＜x＜1，即可得到一个关于a、b的方程组，即可求解．
解答 解：$\left\{\begin{array}{l}{2x-a+b＜1…①}\\{x-2（b-2a）＞3…②}\end{array}\right.$，
解①得：x＜$\frac{a-b+1}{2}$，
解②得：x＞2b+3-4a．
则不等式组的解集是：2b+3-4a＜x＜$\frac{a-b+1}{2}$．
根据题意得：$\left\{\begin{array}{l}{2b+3-4a=-1}\\{\frac{a-b+1}{2}=1}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$．
点评 本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．还可以观察不等式的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
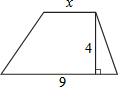如图所示，梯形上底的长是x，下底的长是9，高是4，梯形面积y与底长x之间的关系式是y=2x+18．
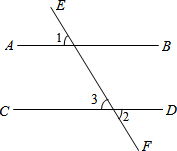推理说明题，按图填空，括号内注明理由．
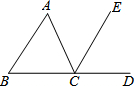写出图中∠B的一个同位角∠ECD或∠ACD．