Question

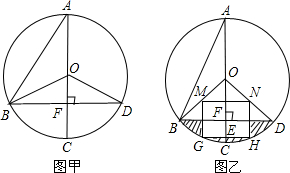
如图甲，已知在⊙O中，AB=4

3

，AC是⊙O的直径，AC⊥BD于F，∠A=30度．
（1）连接BC，CD，请你判定四边形OBCD是何种特殊的四边形？试说明理由；
（2）若用扇形OBD围成一个圆锥侧面，请出这个圆锥的底面圆的半径；
（3）如图乙，若将“∠A=30°”改为“∠A=22.5°”，其余条件不变，以半径OB、OD的中点M、N为顶点作矩形MNGH，顶点G、H在⊙O的劣弧

BD

上，GH交OC于点E．试求图中阴影部分的面积．（结果保留π）

Answer 1

（1）四边形OBCD是菱形．
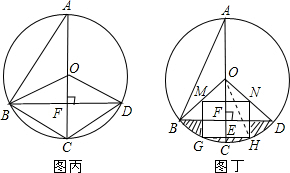
如图丙，∵AC⊥BD，AC是直径，
∴AC垂直平分BD．
∴BF=FD，

BC

=

CD

．
∴∠BAD=2∠BAC=60°，
∴∠BOD=120°．
∵BF=

1

2

AB=2

3

，
在Rt△ABF中，
AF=

AB2-BF2

=

(4 3 )2-(2 3 )2

=

36

=6．
在Rt△BOF中，
∴OB²=BF²+OF²．即(2

3

)2+(6-OB)2=OB2．
解得：OB=4．
∵OA=OB=4，
∴OF=AF-AO=6-4=2，
∵AC=2OA=8，
∴CF=AC-AF=8-6=2，
∴CF=OF，
∵BF=FD，AC⊥BD，
∴四边形OBCD是菱形；

（2）设圆锥的底面圆的半径为r，则周长为2πr．
∵扇形OBD的弧长=

120

180

π•4=

8

3

π，
∴2πr=

8

3

π，
解得：r=

4

3

；

（3）如图丁，连接OH．
∵∠A=22.5°，
∴∠BOC=45°，
∵∠BOD=∠BOC=90°，OB=OD=4，
∴BD=

2

OB=4

2

，
∴OF=

1

2

BD=2

2

，
∵M、N是OB、OD的中点，
∴MN=

1

2

BD=

1

2

×4

2

=2

2

，
∵四边形MNGH是矩形，
∴MN=GH=2

2

，EH=EG=

1

2

MN=

2

，
在Rt△HOE中，OE²=OH²-HE²，即OE²=4²-（

2

）²，
解得：OE=

14

，
∴EF=OE-OF=

14

-2

2

，
∵扇形OBD的面积=

1

2

lR=

1

2

×

8

3

π×4=

16

3

π，
∴图中阴影部分的面积=

16

3

π-

1

2

×4×4-（

14

-2

2

）×2

2

=

16

3

π-8-4

7

+8
=

16

3

π-4

7

．