题目内容
18.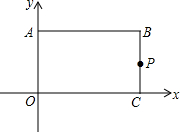 如图,矩形ABCO的两边AO=3,AB=4,以顶点O为原点,OC、OA所在直线分别为x轴、y轴建立如图所示平面直角坐标系,P是线段BC上一动点,设PC=m,已知点D在第一象限,且位于直线y=x+3上,若△APD是等腰直角三角形,则点D的坐标为(2,5)或(4,7).
如图,矩形ABCO的两边AO=3,AB=4,以顶点O为原点,OC、OA所在直线分别为x轴、y轴建立如图所示平面直角坐标系,P是线段BC上一动点,设PC=m,已知点D在第一象限,且位于直线y=x+3上,若△APD是等腰直角三角形,则点D的坐标为(2,5)或(4,7).
分析 首先求得直线y=x+3与x轴,y轴分别交于(-3,0)(0,3),于是得到∠AEC=45°,根据矩形的性质得到AB∥OC,于是得到∠DAB=45°,若∠ADB=90°,则∠DAP=45°,推出P与B重合,由于D在AB的垂直平分线上,于是求得D的横坐标为2,由于点D在直线y=x+3上,即可得到D(2,5),若∠APD=90°,则∠DAP=45°,推出D在CB的延长线上,于是求得D(4,7).
解答 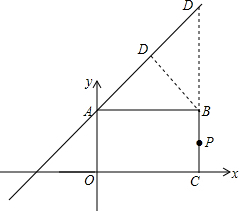 解:直线y=x+3与x轴,y轴分别交于(-3,0)(0,3),
解:直线y=x+3与x轴,y轴分别交于(-3,0)(0,3),
∴∠AEC=45°,
∵四边形AOCB是矩形,
∴AB∥OC,
∴∠DAB=45°,
若∠ADB=90°,
则∠DAP=45°,
∴P与B重合,
∴D在AB的垂直平分线上,
∵AB=4,
∴D的横坐标为2,
∵点D在直线y=x+3上,
∴D(2,5),
若∠APD=90°,
则∠DAP=45°,
∴D在CB的延长线上,
∴D(4,7),
∴若△APD是等腰直角三角形,则点D的坐标为(2,5)或(4,7).
故答案为:(2,5)或(4,7).
点评 本题考查了矩形的性质,等腰直角三角形的判定,一次函数图象上点的坐标特征,正确的画出图形是解题的关键.

练习册系列答案
相关题目
8.下列计算正确的是( )
| A. | x4+x2=x6 | B. | x4÷x2=x2 | C. | 3a2-a2=2 | D. | (2a2)2=2a4 |
6.已知反比例函数y=$\frac{k}{x}$的图象在第二、四象限内,函数图象上有两点A(6,y1),B(5,y2),则y1与y2的大小关系为( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
7.一个正六边形绕着它的中心旋转,使其与本身完全重合,则至少要旋转( )
| A. | 45° | B. | 60° | C. | 90° | D. | 120° |