题目内容
10.如图甲所示,AD是△ABC的中线,CF⊥AD于F,BE⊥AD交AD的延长线于E,求证:CF=BF,中点D到E,F的距离DE,DF是否相等?(1)如图乙,将中线AD改为射线AM,那么“DE=DF”还成立吗?
(2)如图丙,将中线AD改为△ABC外一点射线AM,那么“DE=DF”还成立吗?
(3)如图丁“射线AM”改为“射线MN”,射线MN不过顶点A,那么“DE=DF”还成立吗?
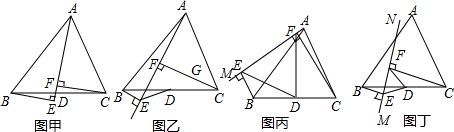
分析 如图甲,根据AD是△ABC的中线,得到BD=CD,即可证明△BDE≌△CDF,根据全等三角形对应边相等的性质即可得到结论;
(1)如图乙,连接DF,延长ED交CF于G,由CF⊥AM于F,BE⊥AM,得到BE∥CF,根据平行线的性质得到∠BED=∠CGD,推出△BDE≌△CDG,根据全等三角形的性质得到DE=DG,然后由直角三角形的性质即可得到结论;
(2)如图丙,方法同(1);
(3)如图丁,方法同(1).
解答 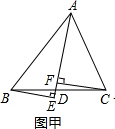 如图甲,证明:∵AD是△ABC的中线,
如图甲,证明:∵AD是△ABC的中线,
∴BD=CD,
在△BDE和△CDF中,
$\left\{\begin{array}{l}{∠BED=∠CFD=90°}\\{∠BDE=∠CDF}\\{BD=CD}\end{array}\right.$,
∴△BDE≌△CDF(AAS),
∴BE=CF,DE=DF;
(1)如图乙,连接DF,延长ED交CF于G,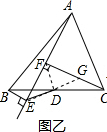
∵CF⊥AM于F,BE⊥AM,
∴BE∥CF,
∴∠BED=∠CGD,
在△BDE和△CDG中,$\left\{\begin{array}{l}{∠BED=∠DGC}\\{∠BDE=∠CDG}\\{BD=CD}\end{array}\right.$,
∴△BDE≌△CDG,
∴DE=DG,
∵∠EFG=90°,
∴DF=DE=$\frac{1}{2}$EG;
(2)如图丙,延长ED交FC的延长线于G,
∵CF⊥AM于F,BE⊥AM,
∴∠BED=∠CGD,
在△BDE和△CDG中,$\left\{\begin{array}{l}{∠BED=∠DGC}\\{∠BDE=∠CDG}\\{BD=CD}\end{array}\right.$,
∴△BDE≌△CDG,
∴DE=DG,
∵∠EFG=90°,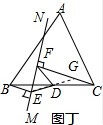
∴DF=DE=$\frac{1}{2}$EG;
(3)如图丁,延长ED交CF于G,
∵CF⊥AM于F,BE⊥AM,
∴BE∥CF,
∴∠BED=∠CGD,
在△BDE和△CDG中,$\left\{\begin{array}{l}{∠BED=∠DGC}\\{∠BDE=∠CDG}\\{BD=CD}\end{array}\right.$,
∴△BDE≌△CDG,
∴DE=DG,
∵∠EFG=90°,
∴DF=DE=$\frac{1}{2}$EG;
点评 本题考查了全等三角形的判定和性质,直角三角形的性质,平行线的判定和性质,本题中求证△BDE≌△CDG是解题的关键.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 从正面看如图所示的几何体,得到的平面图形是( )
从正面看如图所示的几何体,得到的平面图形是( )| A. |  | B. |  | C. |  | D. |  |
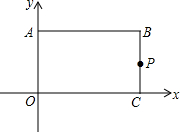 如图,矩形ABCO的两边AO=3,AB=4,以顶点O为原点,OC、OA所在直线分别为x轴、y轴建立如图所示平面直角坐标系,P是线段BC上一动点,设PC=m,已知点D在第一象限,且位于直线y=x+3上,若△APD是等腰直角三角形,则点D的坐标为(2,5)或(4,7).
如图,矩形ABCO的两边AO=3,AB=4,以顶点O为原点,OC、OA所在直线分别为x轴、y轴建立如图所示平面直角坐标系,P是线段BC上一动点,设PC=m,已知点D在第一象限,且位于直线y=x+3上,若△APD是等腰直角三角形,则点D的坐标为(2,5)或(4,7).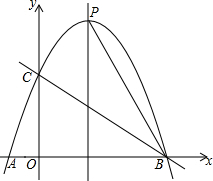 如图,抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3)三点,对称轴与抛物线相交于点P、与直线BC相交于M,连接PB.
如图,抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3)三点,对称轴与抛物线相交于点P、与直线BC相交于M,连接PB.