题目内容
6.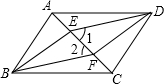 (1)如图,四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接ED,BF.求证:∠1=∠2.
(1)如图,四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接ED,BF.求证:∠1=∠2.(2)已知y与x+2成正比例,且当x=1时,y=-6,求y与x的函数关系式.
分析 (1)根据平行四边形的对边平行且相等,得AB=CD,AB∥CD,再根据平行线的性质,得∠BAE=∠DCF,∠AEB=∠CFD,由AAS证明△ABE≌△CDF,根据全等三角形的对应边相等,得BE=DF,从而得出四边形BFDE是平行四边形,根据两直线平行内错角相等证得∠1=∠2;
(2)根据y与x+2成正比例关系设出函数的解析式,再把当x=1时,y=-6代入函数解析式即可求出k的值,进而求出y与x之间的函数解析式.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∵BE∥DF,
∴∠BEF=∠EFD,
又∠BEF+∠AEB=180°,
∠EFD+∠DFC=180°,
∴∠AEB=∠CFD,
在△ABE与△CDF中,$\left\{\begin{array}{l}{∠AEB=∠CFD}\\{∠BAE=∠DCF}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△CDF,
∴BE=DF,
又BE∥DF,
∴四边形BFDE是平行四边形,
∴DE∥BF,
∴∠1=∠2;
(2)解:∵y与x+2成正比例
∴可设y=k(x+2),把当x=1时,y=-6.代入得-6=k(1+2).
解得:k=-2.
故y与x的函数关系式为y=-2x-4.
点评 本题考查的是利用平行四边形的性质,全等三角形的判定与性质,待定系数法求一次函数解析式,以及一次函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
14.已知2a=3b(ab≠0),则下列比例式成立的是( )
| A. | $\frac{a}{2}$=$\frac{3}{b}$ | B. | $\frac{a}{3}$=$\frac{b}{2}$ | C. | $\frac{a}{b}$=$\frac{2}{3}$ | D. | $\frac{b}{a}$=$\frac{3}{2}$ |
14.因式分解x3-2x2+x正确的是( )
| A. | (x-1)2 | B. | x (x-1)2 | C. | x( x2-2x+1) | D. | x (x+1)2 |
1.下列计算正确的是( )
| A. | (a4)3=a7 | B. | a8÷a4=a2 | C. | (ab)3=a3b3 | D. | (a+b)2=a2+b2 |
11.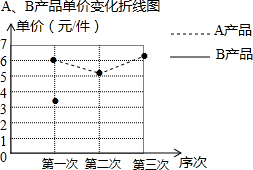 某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
A,B产品单价变化统计表
并求得了A产品三次单价的平均数和方差:
$\overline{{x}_{A}}$=5.9,SA2=$\frac{1}{3}$[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=$\frac{43}{150}$
(1)在折线图中画出B产品的单价变化的情况;
(2)求B产品三次单价的方差;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件的基础上调m%(m>0),但调价后不能超过4元/件,并且使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
 某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.A,B产品单价变化统计表
| 第一次 | 第二次 | 第三次 | |
| A产品单价(元/件) | 6 | 5.2 | 6.5 |
| B产品单价(元/件) | 3.5 | 4 | 3 |
$\overline{{x}_{A}}$=5.9,SA2=$\frac{1}{3}$[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=$\frac{43}{150}$
(1)在折线图中画出B产品的单价变化的情况;
(2)求B产品三次单价的方差;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件的基础上调m%(m>0),但调价后不能超过4元/件,并且使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
18.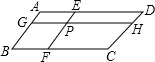 如图,在平行四边形ABCD中,过点P作直线EF、GH分别平行于AB、BC,那么图中共有( )平行四边形.
如图,在平行四边形ABCD中,过点P作直线EF、GH分别平行于AB、BC,那么图中共有( )平行四边形.
 如图,在平行四边形ABCD中,过点P作直线EF、GH分别平行于AB、BC,那么图中共有( )平行四边形.
如图,在平行四边形ABCD中,过点P作直线EF、GH分别平行于AB、BC,那么图中共有( )平行四边形.| A. | 4个 | B. | 5个 | C. | 8个 | D. | 9个 |
15.已知甲、乙两数的和是6,甲数是乙数的3倍,设甲数为x,乙数为y,根据题意,列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=6}\\{x=3y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=6}\\{y=3x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+2y=6}\\{x=3y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=6}\\{y=3x}\end{array}\right.$ |