题目内容
19.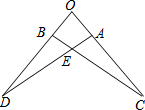 如图,△OAD≌△OBC,且∠O=80°,∠C=20°,则∠AEB=120°.
如图,△OAD≌△OBC,且∠O=80°,∠C=20°,则∠AEB=120°.
分析 根据全等三角形的性质求出∠D,根据三角形外角性质求出∠DBC,再根据三角形的外角性质求出即可.
解答 解:∵△OAD≌△OBC,∠C=20°,
∴∠D=∠C=20°,
∵∠O=80°,
∴∠DBC=∠O+∠C=100°,
∴∠AEB=∠D+∠DBC=20°+100°=120°,
故答案为:120.
点评 本题考查了三角形的外角性质,全等三角形的性质的应用,能根据全等三角形的性质得出∠D=∠C是解此题的关键,注意:全等三角形的对应角相等,对应边相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.甲、乙两个仓阵要向A、B两地调运小麦.甲可以调出80吨.乙可以调出40吨.A地需要小麦50吨,B需要70吨.
运费如表一:(单位:千米)
运费如表二:(单位:元/吨 千米)
(1)设甲库运往A地x(20≤x≤40)吨求总运费(甲、乙两个仓库的运费之和)y与x之间的函数关系式;
(2)根据(1)中的函数的增减性以及x的取值范围,请确定运费最少的运送方案.
运费如表一:(单位:千米)
| A | B | |
| 甲 | 50 | 40 |
| 乙 | 80 | 25 |
| A | B | |
| 甲 | 2 | 1 |
| 乙 | 1.5 | 2 |
(2)根据(1)中的函数的增减性以及x的取值范围,请确定运费最少的运送方案.
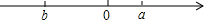 对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a-b|.
对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a-b|.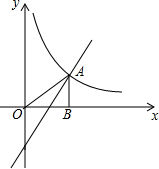 一次函数y=kx-1与反比例函数y=$\frac{k}{x}$的图象在第一象限交于点A,过点A作AB⊥x轴于点B,已知S△AOB=1,求反比例函数及一次函数的表达式.
一次函数y=kx-1与反比例函数y=$\frac{k}{x}$的图象在第一象限交于点A,过点A作AB⊥x轴于点B,已知S△AOB=1,求反比例函数及一次函数的表达式. 如图,A、C两乡镇到水渠边l的距离分别为AB=2km,CD=4km,且BD=8km.
如图,A、C两乡镇到水渠边l的距离分别为AB=2km,CD=4km,且BD=8km.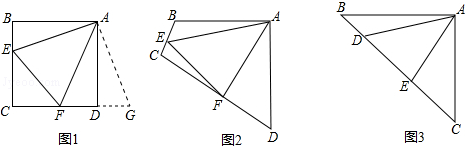
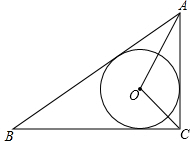 如图所示,⊙O内切于△ABC,若∠ACB=90°,∠AOC=105°,AB=$\frac{8}{3}$,求AC及S△ABC.
如图所示,⊙O内切于△ABC,若∠ACB=90°,∠AOC=105°,AB=$\frac{8}{3}$,求AC及S△ABC.