题目内容
7.正六边形的内切圆半径为$\sqrt{3}$,则该正六边形的边长是( )| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 2 | D. | 3 |
分析 根据题意画出图形,利用正六边形中的等边三角形的性质求解即可.
解答 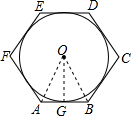 解:如图,连接OA、OB,OG;
解:如图,连接OA、OB,OG;
∵六边形ABCDEF是边长等于正六边形的半径,设正六边形的半径为a,
∵∠AOB=$\frac{360°}{6}$=60°,OA=OB,
∴△OAB是等边三角形,
∴OA=AB=a,
∴OG=OA•sin60°=a×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
解得:a=2,
∴正六边形的边长=2;
故选:C.
点评 此题主要考查了正多边形和圆、等边三角形的判定与性质及特殊角的三角函数值;熟练掌握正六边形的性质,证明△OAB是等边三角形是解决问题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
18.不等式组$\left\{\begin{array}{l}{5x-2<3(x+2)}\\{\frac{2x-1}{3}-\frac{5x+1}{2}≤1}\end{array}\right.$的最大整数解为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.下列说法正确的是( )
| A. | 随机抛掷一枚硬币,反面一定朝上 | |
| B. | 数据3,3,5,5,8的众数是8 | |
| C. | 某商场抽奖活动获奖的概率为$\frac{1}{50}$,说明毎买50张奖券中一定有一张中奖 | |
| D. | 想要了解长沙市民对“全面二孩”政策的看法,宜采用抽样调查 |
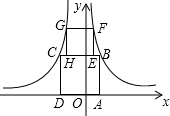 如图,四边形ABCD与EFGH均为正方形,点B、F在函数y=$\frac{1}{x}$(x>0)的图象上,点G、C在函数y=-$\frac{3}{x}$(x<0)的图象上,点A、D在x轴上,点H、E在线段BC上,则点G的纵坐标$\sqrt{5}$+1.
如图,四边形ABCD与EFGH均为正方形,点B、F在函数y=$\frac{1}{x}$(x>0)的图象上,点G、C在函数y=-$\frac{3}{x}$(x<0)的图象上,点A、D在x轴上,点H、E在线段BC上,则点G的纵坐标$\sqrt{5}$+1.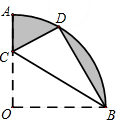 如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,则有下列选项:
如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,则有下列选项: