题目内容
8.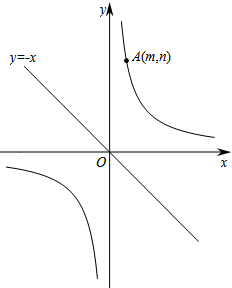 如图,已知直线y=-x和双曲线$y=\frac{k}{x}$(k>0),点A(m,n)(m>0)在双曲线$y=\frac{k}{x}$上.
如图,已知直线y=-x和双曲线$y=\frac{k}{x}$(k>0),点A(m,n)(m>0)在双曲线$y=\frac{k}{x}$上.(1)当m=n=2时,
①直接写出k的值;
②将直线y=-x作怎样的平移能使平移后的直线与双曲线$y=\frac{k}{x}$只有一个交点.
(2)将直线y=-x绕着原点O旋转,设旋转后的直线与双曲线$y=\frac{k}{x}$交于点B(a,b)(a>0,b>0)和点C.设直线AB,AC分别与x轴交于D,E两点,试问:$\frac{AB}{AD}$与$\frac{AC}{AE}$的值存在怎样的数量关系?请说明理由.
分析 (1)①当m=n=2时,得出A(2,2),把点A(2,2)代入双曲线$y=\frac{k}{x}$(k>0)求出k的值即可;
②设平移后的直线解析式为y=-x+b1,由直线和双曲线解析式组成方程组,整理可得方程:x2-b1x+4=0,当判别式=0时,求出b1=±4即可;
(2)分两种情况讨论:由双曲线的对称性可知,C(-a,-b),①当点A在直线BC的上方时,过A、B、C分别作y轴的垂线,垂足分别为F、G、H,则OF=n,OG=OH=b,得出FG=OF-OG=n-b,FH=OF+OH=n+b,由平行线得出比例式,即可得出结论;
②当点A在直线BC的下方时,同理可得出结论;即可得出结果.
解答 解:(1)①当m=n=2时,A(2,2),
把点A(2,2)代入双曲线$y=\frac{k}{x}$(k>0)得:k=2×2=4;
②设平移后的直线解析式为y=-x+b1,
由$\left\{\begin{array}{l}y=-x+{b_1}\\ y=\frac{k}{x}\end{array}\right.$可得,$-x+{b_1}=\frac{4}{x}$,
整理可得:x2-b1x+4=0,
当$△={(-{b_1})^2}-4×1×4=0$,即b1=±4时,方程x2-b1x+4=0有两个相等的实数根,此时直线y=-x+b1与双曲线只有一个交点,
∴只要将直线y=-x向上或向下平移4个单位长度,所得到的直线与双曲线只有一个交点; (2)$\frac{AC}{AE}±\frac{AB}{AD}=2$,理由如下:
(2)$\frac{AC}{AE}±\frac{AB}{AD}=2$,理由如下:
分两种情况讨论:由双曲线的对称性可知,C(-a,-b)
①当点A在直线BC的上方时,如图所示:
过A、B、C分别作y轴的垂线,垂足分别为F、G、H,
则OF=n,OG=OH=b,
∴FG=OF-OG=n-b,FH=OF+OH=n+b,
∵AF∥BG∥x轴,
∴$\frac{AB}{AD}$=$\frac{FG}{FO}$=$\frac{n-b}{n}$,
∵AF∥x轴∥CH,
∴$\frac{AC}{AE}$=$\frac{FH}{FO}$=$\frac{n+b}{n}$,
∴$\frac{AC}{AE}$+$\frac{AB}{AD}$=$\frac{n-b}{n}$+$\frac{n+b}{n}$=2;
②当点A在直线BC的下方时,
同理可求:$\frac{AB}{AD}$=$\frac{b-n}{n}$,$\frac{AC}{AE}$=$\frac{n+b}{n}$,
∴$\frac{AC}{AE}$-$\frac{AB}{AD}$=$\frac{n+b}{n}$-$\frac{b-n}{n}$=2;
综上所述,$\frac{AC}{AE}±\frac{AB}{AD}=2$.
点评 本题是反比例函数综合题目,考查了反比例函数解析式的求法、直线与双曲线的交点坐标、根的判别式、平行线分线段成比例定理等知识;本题综合性强,有一定难度.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案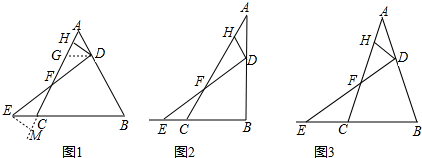
 如图,甲、乙是两个不透明的圆桶,甲桶内的三张牌分别标记数字2,3,4乙桶内的两张分别标记数字1,2(这些牌除所标数字不同外,其余均相同).若小宇从甲乙两个圆桶中各随机抽出一张牌,其数字之和大于4的概率是$\frac{1}{2}$.
如图,甲、乙是两个不透明的圆桶,甲桶内的三张牌分别标记数字2,3,4乙桶内的两张分别标记数字1,2(这些牌除所标数字不同外,其余均相同).若小宇从甲乙两个圆桶中各随机抽出一张牌,其数字之和大于4的概率是$\frac{1}{2}$.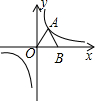 如图,等边△OAB的边长为2,点B在x轴上,点A在双曲线y=$\frac{k}{x}$(k≠0)上,将△OAB绕点O顺时针旋转α度(0<α<360°),使点A仍落在双曲线y=$\frac{k}{x}$(k≠0)上,则α的值不可能是( )
如图,等边△OAB的边长为2,点B在x轴上,点A在双曲线y=$\frac{k}{x}$(k≠0)上,将△OAB绕点O顺时针旋转α度(0<α<360°),使点A仍落在双曲线y=$\frac{k}{x}$(k≠0)上,则α的值不可能是( ) 在等腰三角形ABC中,AB=AC,O为AB上一点,以O为圆心,OB长为半径的圆交BC于D,DE⊥AC交AC于E.
在等腰三角形ABC中,AB=AC,O为AB上一点,以O为圆心,OB长为半径的圆交BC于D,DE⊥AC交AC于E.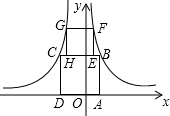 如图,四边形ABCD与EFGH均为正方形,点B、F在函数y=$\frac{1}{x}$(x>0)的图象上,点G、C在函数y=-$\frac{3}{x}$(x<0)的图象上,点A、D在x轴上,点H、E在线段BC上,则点G的纵坐标$\sqrt{5}$+1.
如图,四边形ABCD与EFGH均为正方形,点B、F在函数y=$\frac{1}{x}$(x>0)的图象上,点G、C在函数y=-$\frac{3}{x}$(x<0)的图象上,点A、D在x轴上,点H、E在线段BC上,则点G的纵坐标$\sqrt{5}$+1.