题目内容
10. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=$\sqrt{2}$,CE=3$\sqrt{2}$,H是AF的中点,那么CH的长是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=$\sqrt{2}$,CE=3$\sqrt{2}$,H是AF的中点,那么CH的长是( )| A. | 3.5 | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{5}$ |
分析 根据正方形的性质求出AB=BC=$\sqrt{2}$,CE=EF=3$\sqrt{2}$,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=4$\sqrt{2}$,FM=2$\sqrt{2}$,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH=$\frac{1}{2}$AF,根据勾股定理求出AF即可.
解答 解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=$\sqrt{2}$,CE=3$\sqrt{2}$,
∴AB=BC=$\sqrt{2}$,CE=EF=3$\sqrt{2}$,∠E=90°,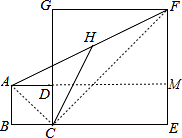 延长AD交EF于M,连接AC、CF,
延长AD交EF于M,连接AC、CF,
则AM=BC+CE=4$\sqrt{2}$,FM=EF-AB=2$\sqrt{2}$,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH=$\frac{1}{2}$AF,
在Rt△AMF中,由勾股定理得:AF=$\sqrt{A{M}^{2}+F{M}^{2}}$=2$\sqrt{10}$,
∴CH=$\sqrt{10}$,
故选:C.
点评 本题考查了勾股定理,正方形的性质,直角三角形斜边上的中线的应用,解此题的关键是能正确作出辅助线,并求出AF的长和得出CH=$\frac{1}{2}$AF,有一定的难度.

练习册系列答案
相关题目
20.已知A样本的数据如下:72,73,76,76,77,78,78,78,B样本的数据恰好是A样本数据每个的2倍,则A,B两个样本的方差关系是( )
| A. | B是A的$\sqrt{2}$倍 | B. | B是A的2倍 | C. | B是A的4倍 | D. | 一样大 |
5.下列各计算中,正确的是( )
| A. | (a3)2=a6 | B. | a3•a2=a6 | C. | a8÷a2=a4 | D. | a+2a2=3a2 |
 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中成立的有①②③.(只填序号)
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中成立的有①②③.(只填序号)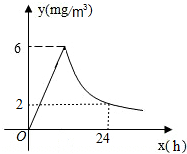 每年春季为预防流感,某校利用休息日对教室进行药熏消毒,已知药物燃烧过程及燃烧完后空气中的含药量y(mg/m3)与时间x(h)之间的关系如图所示,根据消毒要求,空气中的含药量不低于3mg/m3且持续时间不能低于10h.请你帮助计算一下,当空气中的含药量不低于3mg/m3时,持续时间可以达到12h.
每年春季为预防流感,某校利用休息日对教室进行药熏消毒,已知药物燃烧过程及燃烧完后空气中的含药量y(mg/m3)与时间x(h)之间的关系如图所示,根据消毒要求,空气中的含药量不低于3mg/m3且持续时间不能低于10h.请你帮助计算一下,当空气中的含药量不低于3mg/m3时,持续时间可以达到12h.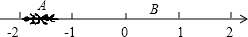 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m.
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m.