题目内容
1.计算:$\sqrt{\frac{1}{5}}+2\sqrt{20}-4\sqrt{\frac{4}{5}}-\frac{1}{5}\sqrt{5}$.分析 利用二次根式的性质化简二次根式进而合并求出即可.
解答 解:$\sqrt{\frac{1}{5}}+2\sqrt{20}-4\sqrt{\frac{4}{5}}-\frac{1}{5}\sqrt{5}$
=$\frac{\sqrt{5}}{5}$+4$\sqrt{5}$-4×2×$\frac{\sqrt{5}}{5}$-$\frac{\sqrt{5}}{5}$,
=$\frac{12}{5}\sqrt{5}$.
点评 此题主要考查了二次根式的加减,正确化简二次根式是解题关键.

练习册系列答案
相关题目
12.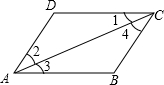 如图所示,下列推理及所注理由正确的是( )
如图所示,下列推理及所注理由正确的是( )
 如图所示,下列推理及所注理由正确的是( )
如图所示,下列推理及所注理由正确的是( )| A. | 因为∠1=∠3,所以AB∥CD(两直线平行,内错角相等) | |
| B. | 因为AB∥CD,所以∠2=∠4(两直线平行,内错角相等) | |
| C. | 因为AD∥BC,所以∠3=∠4(两直线平行,内错角相等) | |
| D. | 因为∠2=∠4,所以AD∥BC(内错角相等,两直线平行) |
9.下列四个命题:①两数之和大于两数之差;②钝角的补角是锐角;③一个数的绝对值总大于这个数本身;④在一个平面内如果直线a⊥直线b,直线b⊥直线c,那么直线a⊥直线c.其中假命题是( )
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
10.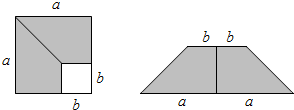 如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
 如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )| A. | (a-b)2=a2-2ab+b2 | B. | (a+b)2=a2+2ab+b2 | C. | a2-b2=(a+b)(a-b) | D. | 无法确定 |
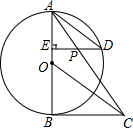 如图,AB是⊙O的直径,BC切⊙O于点B,OC平行于弦AD,过点D作DE⊥AB于点E,连结AC,与DE交于点P.求证:
如图,AB是⊙O的直径,BC切⊙O于点B,OC平行于弦AD,过点D作DE⊥AB于点E,连结AC,与DE交于点P.求证: 如图所示,一块长方形地板,长为60cm,宽为40cm,上面横竖各有两道宽为5cm的花纹(图中阴影部分),那么空白部分的面积是多少?
如图所示,一块长方形地板,长为60cm,宽为40cm,上面横竖各有两道宽为5cm的花纹(图中阴影部分),那么空白部分的面积是多少? 如图,直线AB与CD相交于点D,且∠AOC+∠BOD=140°,则∠AOD等于110°.
如图,直线AB与CD相交于点D,且∠AOC+∠BOD=140°,则∠AOD等于110°.