题目内容
20. 如图,在平面直角坐标系中,将长方形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(5,4),则点E的纵坐标为$\frac{3}{2}$.
如图,在平面直角坐标系中,将长方形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(5,4),则点E的纵坐标为$\frac{3}{2}$.
分析 根据折叠的性质得到AF=AD=5,根据勾股定理求出OF,得到FC,设EC=x,根据勾股定理列出方程,解方程即可.
解答 解:由折叠的性质可知,AF=AD=5,
由勾股定理得,OF=$\sqrt{A{F}^{2}-O{A}^{2}}$=3,
∴FC=OC-OF=2,
设EC=x,则EF=ED=4-x,
由勾股定理得,(4-x)2=x2+22,
解得,x=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题考查的是翻转变换的性质、矩形的性质、坐标与图形的变化,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
5.对于一组数据-1,4,-1,2下列结论不正确的是( )
| A. | 平均数是1 | B. | 众数是-1 | C. | 中位数是0.5 | D. | 方差是3.5 |
12.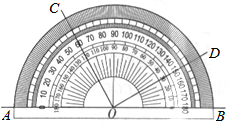 如图所示,用量角器度量一些角的度数.下列结论中正确的是( )
如图所示,用量角器度量一些角的度数.下列结论中正确的是( )
 如图所示,用量角器度量一些角的度数.下列结论中正确的是( )
如图所示,用量角器度量一些角的度数.下列结论中正确的是( )| A. | ∠BOC=60° | B. | ∠COD=150° | ||
| C. | ∠AOC与∠BOD的大小相等 | D. | ∠AOC与∠BOD互余 |
9.若a<0,b>0,化简|a|+|2b|-|a-b|得( )
| A. | b | B. | -b | C. | -3b | D. | 2a+b |
10.下面四个等式的变形中正确的是( )
| A. | 由4x+8=0得x+2=0 | B. | 由x+7=5-3x得4x=2 | ||
| C. | 由$\frac{3}{5}$x=4得x=$\frac{12}{5}$ | D. | 由-4(x-1)=-2得4x=-6 |
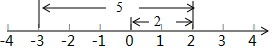 如图所示,一个点从数轴上的原点开始,先向右移动2个单位长度,再向左移动5个单位长度,可以看到终点表示是-3,已知A、B是数轴上的点,请参照图并思考,完成下列各题.
如图所示,一个点从数轴上的原点开始,先向右移动2个单位长度,再向左移动5个单位长度,可以看到终点表示是-3,已知A、B是数轴上的点,请参照图并思考,完成下列各题.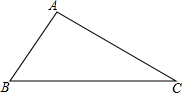 如图,在△ABC中,∠B=55°,∠C=30°.
如图,在△ABC中,∠B=55°,∠C=30°.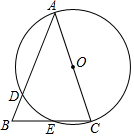 如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交AB于点E.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交AB于点E.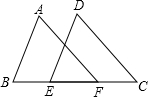 如图,若AB=DE,BE=CF,要证△ABF≌△DEC,需补充条件AF=DC(填写一个即可).
如图,若AB=DE,BE=CF,要证△ABF≌△DEC,需补充条件AF=DC(填写一个即可).