题目内容
18．已知不等边三角形ABC的三边长分别为整数a，b，c，且满足a2+b2-4a-6b+13=0，求c的长．分析 由a2+b2-6a-4b+13=0，得（a-3）2+（b-2）2=0，求得a、b的值，再根据三角形的三边关系定理，得|a-b|＜c＜a+b，求得c即可．
解答 解：∵a2+b2-6a-4b+13=0，∴（a-3）2+（b-2）2=0，
∴a-3=0，b-2=0，
解得a=3，b=2，
∵1＜c＜5，
∴c=4，
即c的长为4．
点评 此题考查了配方法的应用，三角形的三边关系，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
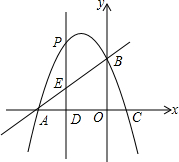在平面直角坐标系中，直线y=x+4与x轴分别交于A、B两点，抛物线y=-x2+bx+c经过A、B两点，并于x轴交于另一点C（点C在点A的右侧），点P是抛物线上一动点．