题目内容
18．若x2+x-5=0，则$\frac{{x}^{2}-x-6}{x-3}$÷$\frac{x+3}{{x}^{2}+2x-3}$的值为3．分析 把（x2+x）看作一个整体并求出其值，然后代入化简后的分式进行计算即可得解．
解答 解：$\frac{{x}^{2}-x-6}{x-3}$÷$\frac{x+3}{{x}^{2}+2x-3}$
=$\frac{（x+2）（x-3）}{x-3}×\frac{（x-1）（x+3）}{x+3}$
=（x+2）（x-1）
=x2+x-2，
由x2+x-5=0，可得：x2+x=5，
把x2+x=5代入x2+x-2=5-2=3．
故答案为：3
点评 本题考查了分式化简求值，整体思想的利用是解题的关键．
练习册系列答案
相关题目
6．计算（$\frac{1}{2}$）-3的结果正确的是（ ）
| A． | -$\frac{1}{8}$ | B． | $\frac{1}{8}$ | C． | -8 | D． | 8 |
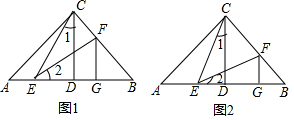【问题情境】一节数学课后，老师布置了一道课后练习题：