题目内容
19.解方程组:$\left\{\begin{array}{l}{3x-y=2}\\{9x+8y=17}\end{array}\right.$.分析 方程组利用加减消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{3x-y=2①}\\{9x+8y=17②}\end{array}\right.$,
①×8+②得:33x=33,即x=1,
把x=1代入①得:y=1,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
10.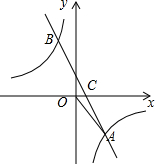 如图,已知点A(3,m),B(-2,6)在反比例函数$y=\frac{k}{x}$的图象上,直线AB与x轴交于点C.
如图,已知点A(3,m),B(-2,6)在反比例函数$y=\frac{k}{x}$的图象上,直线AB与x轴交于点C.
(1)求直线AB的解析式;
(2)若点D在x轴上,且DC=OA,则求点D的坐标.
 如图,已知点A(3,m),B(-2,6)在反比例函数$y=\frac{k}{x}$的图象上,直线AB与x轴交于点C.
如图,已知点A(3,m),B(-2,6)在反比例函数$y=\frac{k}{x}$的图象上,直线AB与x轴交于点C.(1)求直线AB的解析式;
(2)若点D在x轴上,且DC=OA,则求点D的坐标.
14.A、B两地相距160千米,甲车和乙车的平均速度之比为4:5,两车同时从A地出发到B地,乙车比甲车早到30分钟,若求甲车的平均速度,设甲车平均速度为4x千米/小时,则所列方程是( )
| A. | $\frac{160}{4x}$-$\frac{160}{5x}$=30 | B. | $\frac{160}{4x}$-$\frac{160}{5x}$=$\frac{1}{2}$ | C. | $\frac{160}{5x}$-$\frac{160}{4x}$=$\frac{1}{2}$ | D. | $\frac{160}{4x}$+$\frac{160}{5x}$=30 |
6.小米手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共60部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?
A,B两款手机的进货和销售价格如下表:
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共60部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?
A,B两款手机的进货和销售价格如下表:
| A款手机 | B款手机 | |
| 进货价格(元) | 1100 | 1400 |
| 销售价格(元) | 今年的销售价格 | 2000 |
7.为了奖励本次竞赛获奖同学,刘老师用280元买了A、B两种纪念品,A种纪念品每个20元,B种纪念品每个60元,且A种纪念品比B种纪念品多买了2个,设买了A种纪念品x个,B种纪念品y个,你认为下列哪一个方程组适合求两种纪念品各买了多少个?( )
| A. | $\left\{\begin{array}{l}{20x+60y=280}\\{x-y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{60x+20y=280}\\{x-y=2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{20x+60y=280}\\{y-x=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{60x+20y=280}\\{y-x=2}\end{array}\right.$ |
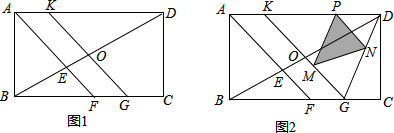
 在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题: 如图,已知O是直线MN上的一点,∠AOB=90°,经过点O的直线DC平分∠BON,∠1=38°,求∠3和∠DOA的度数.
如图,已知O是直线MN上的一点,∠AOB=90°,经过点O的直线DC平分∠BON,∠1=38°,求∠3和∠DOA的度数.