题目内容
14.(1)(x+1)2=36;(2)3(x+5)3=-375.
分析 (1)根据开平方,可得方程的解;
(2)根据开立方,可得方程的解.
解答 解:(1)开平方,得
x+1=6或x+1=-6.
解得x=5或x=-7;
(2)两边都除以3,得
(x+5)3=-125.
开立方,得
x+5=-5.
解得x=-10.
点评 本题考查了立方根,(1)开平方是解题关键,一元二次方程有两个根,以防漏掉;(2)开立方是解题关键.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
2.下列计算正确的是( )
| A. | (-4a-1)(4a-1)=1-16a2 | B. | (x+y)(x2+y2)=x3+y3 | ||
| C. | (-4x)(2x2+3x-1)=-8x3-12x2-4x | D. | (x-2y)2=x2-2xy+4y2 |
4.二元一次方程组$\left\{\begin{array}{l}{2x-y=2}\\{x+y=4}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ |
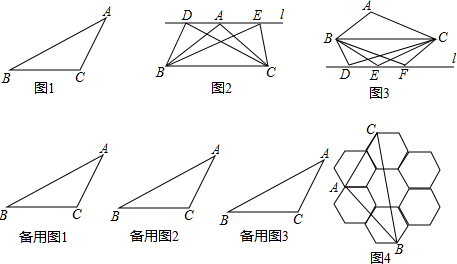
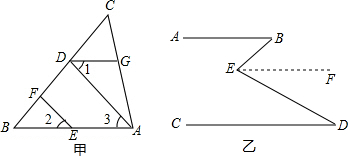 仔细想一想,完成下面的推理过程.
仔细想一想,完成下面的推理过程.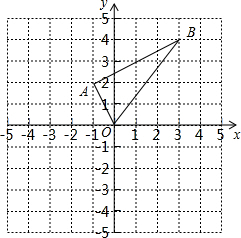 如图在平面直角坐标系中,已知点A(-1,2),B(3,4).
如图在平面直角坐标系中,已知点A(-1,2),B(3,4).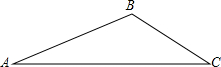 如图,△ABC,AB=18,sinA=$\frac{1}{6}$,sinC=$\frac{1}{3}$,
如图,△ABC,AB=18,sinA=$\frac{1}{6}$,sinC=$\frac{1}{3}$,