题目内容
9.已知△ABC是边长为1的等边三角形,△DBC是以BC为斜边的等腰直角三角形,那么线段AD的长为$\frac{\sqrt{3}+1}{2}$.分析 首先根据题意画出图形,根据AB=AC,DB=DC可证出点A、D都在BC的垂直平分线上,即AD是线段CB的垂直平分线,所以DE=$\frac{1}{2}$BC,AE=$\frac{\sqrt{3}}{2}$AB,再由条件AB=CB=1,可知计算出AD的长.
解答 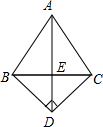 解:根据题意画出可图形,如右图:
解:根据题意画出可图形,如右图:
∵△ABC是等边三角形,
∴AB=AC,
∴点A在BC的垂直平分线上(到线段两端点距离相等的点在线段的垂直平分线上),
∵△DBC是以BC为斜边的等腰直角三角形,
∴DB=DC,
∴点D也在BC的垂直平分线上,
∴AD是线段CB的垂直平分线,
∴AD⊥CB,
∴BE=CE=$\frac{1}{2}$,
∴DE=$\frac{1}{2}$CB=$\frac{1}{2}$,AE=AB•sin60°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
∴AD=AE±DE=$\frac{\sqrt{3}±1}{2}$
故答案为:$\frac{\sqrt{3}+1}{2}$或$\frac{\sqrt{3}-1}{2}$.
点评 此题主要考查了等腰直角三角形,等边三角形的性质,解决此题的关键是证明AD是线段CB的垂直平分线.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
20.如果x,y都不为零,且2x=3y,那么下列比例中正确的是( )
| A. | $\frac{x}{y}=\frac{2}{3}$ | B. | $\frac{x}{3}=\frac{y}{2}$ | C. | $\frac{x}{2}=\frac{3}{y}$ | D. | $\frac{x}{3}=\frac{2}{y}$ |
14.△ABC中,D、E分别是AB和AC边上的中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,则$\overrightarrow{ED}$可表示为( )
| A. | 2$\overrightarrow{a}$ | B. | -2$\overrightarrow{a}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$ |
19.若x<0,那么x+|x|的值为( )
| A. | 正有理数 | B. | 非正有理数 | C. | 零 | D. | 负有理数 |