题目内容
14. 对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,图中的函数是有界函数,其边界是1.
对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,图中的函数是有界函数,其边界是1.(1)直接判断函数y=$\frac{2}{x}$(x>0)和y=-2x+1(-4<x≤2)是不是有界函数?若是有界函数,直接写出其边界值;
(2)若一次函数y=kx+b(-2≤x≤1)的边界值是3,且这个函数的最大值是2,求这个一次函数的解析式;
(3)将二次函数y=-x2(-1≤x≤m,m≥0)的图象向上平移m个单位,得到的函数的边界值是n,当m在什么范围时,满足$\frac{3}{4}$≤n≤1.
分析 (1)在x的取值范围内,y=$\frac{2}{x}$(x>0)的y无最大值,不是有界函数;y=-2x+1(-4<x≤2)是有界函数,其边界值是9;
(2)当k>0时,根据有界函数的定义确定函数过(1,2),(-2,-3)两点;当k<0时,根据有界函数的定义确定函数过(-2,2),(1,-3)两点;利用待定系数法解答即可;
(3)先设m>1,函数向上平移m个单位后,x=0时,y=m,此时边界值t≥1,与题意不符,故m≤1,判断出函数y=-x2所过的点,结合平移,求出0≤m≤$\frac{1}{4}$或$\frac{3}{4}$≤m≤1.
解答 解:(1)y=$\frac{2}{x}$(x>0)不是有界函数;
y=-2x+1(-4<x≤2)是有界函数,
当x=-4时,y=9,当x=2时,y=-3,
∴对于-4<x≤2时,任意函数值都满足-9<y≤9,
∴边界值为9.
(2)当k>0时,由有界函数的定义得函数过(1,2),(-2,-3)两点,设y=kx+b,将(1,2)(-2,-3)代入上式得$\left\{\begin{array}{l}k+b=2\\-2k+b=-3\end{array}\right.$,解得:$\left\{\begin{array}{l}k=\frac{5}{3}\\ b=\frac{1}{3}\end{array}\right.$,所以:y=$\frac{5}{3}$x+$\frac{1}{3}$,
当k<0时,由有界函数的定义得函数过(-2,2),(1,-3)两点,设y=kx+b,将(-2,2),(1,-3)代入上式得$\left\{\begin{array}{l}-2k+b=2\\ k+b=-3\end{array}\right.$,即得$\left\{\begin{array}{l}k=-\frac{5}{3}\\ b=-\frac{4}{3}\end{array}\right.$,函数解析式为y=-$\frac{5}{3}$x-$\frac{4}{3}$.
(3)若m>1,函数向上平移m个单位后,x=0时,y=m,此时边界值t≥1,与题意不符,故m≤1,函数y=-x2过点(-1,-1),(0,0);向上平移m个单位后,平移图象经过(-1,-1+m);(0,m).
∴-1≤-1+m≤-$\frac{3}{4}$或$\frac{3}{4}$≤m≤1,即0≤m≤$\frac{1}{4}$或$\frac{3}{4}$≤m≤1.
点评 本题考查了二次函数综合题,结合新定义,弄清函数边界值的定义,同时要熟悉平移变换的性质.

 如图是某月的日历表,在此日历表上可以用一个矩形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22),若圈出的9个数中,最大数与最小数的积为192,则这9个数的和为( )
如图是某月的日历表,在此日历表上可以用一个矩形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22),若圈出的9个数中,最大数与最小数的积为192,则这9个数的和为( )| A. | 32 | B. | 126 | C. | 135 | D. | 144 |

| A. | 圆锥 | B. | 球 | C. | 圆柱 | D. | 圆 |
 由于现在人们生活水平的普遍提高,大家对自己的生存环境越来越关注,特别是对大气环境质量的关注,而空气中又以PM2.5对人体的危害性最大,某市环保局对该市市民进行了一项民意调查,以了解PM2.5浓度升高时对人们户外活动是否有影响,并制作了统计图表的一部分如下:
由于现在人们生活水平的普遍提高,大家对自己的生存环境越来越关注,特别是对大气环境质量的关注,而空气中又以PM2.5对人体的危害性最大,某市环保局对该市市民进行了一项民意调查,以了解PM2.5浓度升高时对人们户外活动是否有影响,并制作了统计图表的一部分如下:| 公众对于户外活动的态度 | 百分比 |
| A.没有影响 | a |
| B.影响不大,还可以进行户外活动 | 5% |
| C.有影响,减少户外活动 | 42% |
| D.影响很大,尽可能不去户外活动 | b |
| E.不关心这个问题 | 6% |
(2)根据以上信息,请直接补全条形统计图;
(3)若该市约400万人,根据上述信息,请你估计一下持有“影响很大,尽可能不去户外活动”这种态度的约有多少万人.(说明:“PM2.5”是指大气中危害健康的直径小于2.5微米的颗粒物,也称可入肺颗粒物)
 如图,矩形ACBE中,AC=6,BC=8,D是AB上一动点,当AD=$\frac{11}{5}$时,∠BDC=2∠BAE.
如图,矩形ACBE中,AC=6,BC=8,D是AB上一动点,当AD=$\frac{11}{5}$时,∠BDC=2∠BAE.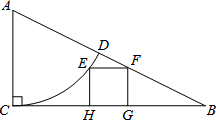 如图,Rt△ABC中,∠ACB=90°,AC=5,CB=10.以点A为圆心,AC长为半径的弧CD交AB于点D,点E是弧CD上任意一点,EH⊥BC于点H,以EH为边长作正方形EHGF,点F在AB边上,则S正方形EFGH=4.
如图,Rt△ABC中,∠ACB=90°,AC=5,CB=10.以点A为圆心,AC长为半径的弧CD交AB于点D,点E是弧CD上任意一点,EH⊥BC于点H,以EH为边长作正方形EHGF,点F在AB边上,则S正方形EFGH=4. 如图,C,F是线段BE上的两点,△ABF≌△DEC,且AC=DF.
如图,C,F是线段BE上的两点,△ABF≌△DEC,且AC=DF. 如图,已知∠ABD=∠ACE,且AD=AE,求证:PB=PC.
如图,已知∠ABD=∠ACE,且AD=AE,求证:PB=PC. 如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,将△ABC折叠,使点B恰好落
如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,将△ABC折叠,使点B恰好落