题目内容
3.在Rt△ABC中,∠C=90°,AC=3,BC=4,以C为圆心,r为半径作⊙C.若⊙C与斜边AB有两个公共点,则r的取值范围是$\frac{12}{5}$<r≤3.分析 作CD⊥AB于D,由勾股定理求出AB,由三角形的面积求出CD,由AC>BC,可得以C为圆心,r=4为半径所作的圆与斜边AB只有一个公共点;若⊙C与斜边AB有两个公共点,即可得出r的取值范围.
解答 解:作CD⊥AB于D,如图所示: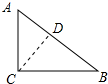
∵∠C=90°,AC=3,BC=4,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵△ABC的面积=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC,
∴CD=$\frac{AC•BC}{AB}$=$\frac{12}{5}$,
即圆心C到AB的距离d=$\frac{12}{5}$,
∵AC<BC,
∴以C为圆心,r=4为半径所作的圆与斜边AB只有一个公共点,
∴若⊙C与斜边AB有两个公共点,则r的取值范围是$\frac{12}{5}$<r≤3.
故答案为:$\frac{12}{5}$<r≤3.
点评 此题考查了直线与圆的位置关系、勾股定理以及直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
14.下列语句中,正确的是( )
| A. | -a一定表示一个负数 | B. | 若a与b互为相反数,则a+b=0 | ||
| C. | m的倒数是$\frac{1}{m}$ | D. | |a|=a |
8. 如图,⊙O的半径为5,直线l是⊙O的切线,A为切点,则点O到直线l的距离是( )
如图,⊙O的半径为5,直线l是⊙O的切线,A为切点,则点O到直线l的距离是( )
 如图,⊙O的半径为5,直线l是⊙O的切线,A为切点,则点O到直线l的距离是( )
如图,⊙O的半径为5,直线l是⊙O的切线,A为切点,则点O到直线l的距离是( )| A. | 2.5 | B. | 3 | C. | 5 | D. | 10 |
13.下列说法正确的是( )
| A. | 有最大的负数,没有最小的整数 | |
| B. | 没有最大的有理数,也没有最小的有理数 | |
| C. | 有最大的负数,没有最小的负数 | |
| D. | 有最小的负数,没有最大的正数 |
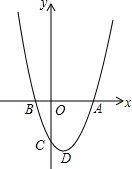 如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D.
如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D. 由8个大小相同的正方体组成一个几何体,如图是分别从正面看和从上面看到的图形,则这个几何体从左面看到的图形是( )
由8个大小相同的正方体组成一个几何体,如图是分别从正面看和从上面看到的图形,则这个几何体从左面看到的图形是( )



 根据要求画图
根据要求画图