题目内容
14.若a2+1=5a,b2+1=5b,且a≠b,则$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=23.分析 由题意可知:a、b是方程x2+1=5x的两个根,然后根据根与系数的关系即可求出答案.
解答 解:由题意可知:a、b是方程x2-5x+1=0的两个根,
∴a+b=5,ab=1,
∴原式=$\frac{{a}^{2}+{b}^{2}}{{a}^{2}{b}^{2}}$=$\frac{(a+b)^{2}-2ab}{{a}^{2}{b}^{2}}$=$\frac{25-2}{1}$=23
故答案为:23
点评 本题考查根与系数的关系,解题的关键是熟练运用根与系数的关系,本题属于基础题型.

练习册系列答案
相关题目
6.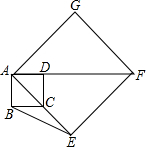 如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )
如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )
 如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )
如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )| A. | $\frac{32\sqrt{2}}{5}$ | B. | $\frac{36\sqrt{2}}{5}$ | C. | $\frac{16\sqrt{5}}{5}$ | D. | $\frac{18\sqrt{5}}{5}$ |
3.在a3•a2•( )=a12中,括号内应填写的代数式是( )
| A. | a7 | B. | a6 | C. | a8 | D. | a3 |
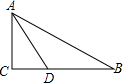 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若∠B=30°,BD=6,则CD的长为3.
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若∠B=30°,BD=6,则CD的长为3.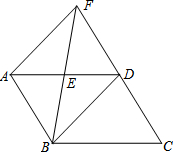 如图,在□ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F,连接BD、AF,BE平分∠ABD,∠ABD=60°.
如图,在□ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F,连接BD、AF,BE平分∠ABD,∠ABD=60°. 如图,在正方形ABCD中,有一个面积为25的小正方形EFGH,其中E、F、G、H分别在AB、BC、FD上,若BF=4,则AB的长为( )
如图,在正方形ABCD中,有一个面积为25的小正方形EFGH,其中E、F、G、H分别在AB、BC、FD上,若BF=4,则AB的长为( )