题目内容
7.某厂计划生产A、B两种产品共50件,已知A产品每件可获利润700元,B产品每件可获利润1200元,设生产A产品的件数为x(件),生产A、B这两种产品获得的总利润为y(元).(1)写出y与x之间的函数表达式;
(2)当x=20时,求y的值.
分析 (1)首先表示出B种产品的数量进而利用A,B种产品的利润进而得出总利润;
(2)把x=20代入(1)中解析式得出答案即可.
解答 解:(1)设生产两种产品的获利总额为y(元),生产A产品x(件),则B种产品共(50-x)件,
因此y与x之间的函数关系式为:y=700x+1200(50-x)=-500x+60000;
(2)当x=20时,y=-500×20+60000=50000.
点评 此题主要考查了一次函数的应用,利用基本数量关系得出y与x的关系式是解题关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
17.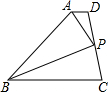 如图,已知四边形ABCD中,AD∥BC,AP平分∠DAB,BP平分∠ABC,它们的交点P给在线段CD上,下面的结论:①AP⊥BP;②点P到直线AD、BC的距离相等;③PD=PC.其中正确的结论有( )
如图,已知四边形ABCD中,AD∥BC,AP平分∠DAB,BP平分∠ABC,它们的交点P给在线段CD上,下面的结论:①AP⊥BP;②点P到直线AD、BC的距离相等;③PD=PC.其中正确的结论有( )
 如图,已知四边形ABCD中,AD∥BC,AP平分∠DAB,BP平分∠ABC,它们的交点P给在线段CD上,下面的结论:①AP⊥BP;②点P到直线AD、BC的距离相等;③PD=PC.其中正确的结论有( )
如图,已知四边形ABCD中,AD∥BC,AP平分∠DAB,BP平分∠ABC,它们的交点P给在线段CD上,下面的结论:①AP⊥BP;②点P到直线AD、BC的距离相等;③PD=PC.其中正确的结论有( )| A. | ①②③ | B. | ①② | C. | 仅① | D. | 仅② |
18.如果单项式-5xa+1y4与2ybx3是同类项,那么a、b的值分别是( )
| A. | a=1,b=4 | B. | a=1,b=3 | C. | a=2,b=4 | D. | a=2,b=3 |
19.一元二次方程x2-mx-2=0的一个根为2,则m的值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,求⊙O的半径.
如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,求⊙O的半径. 如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=105°,求∠DAC的度数.
如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=105°,求∠DAC的度数. 如图,将一张纸条折叠,若∠1=54°,则∠2的度数为72°.
如图,将一张纸条折叠,若∠1=54°,则∠2的度数为72°.