题目内容
17．抛物线y=-x2-6x-8与x轴的交点坐标是（-4，0）、（-2，0），与y轴的交点坐标是（0，-8）．分析 抛物线与x轴交点的纵坐标等于零；抛物线与y轴交点的横坐标等于零．
解答 解：令y=0，则-x2-6x-8=-（x+2）（x+4）=0，
解得x=-4或x=-2，
所以该抛物线与x轴的交点坐标是（-4，0）、（-2，0）．
令x=0，则y=-8，即该抛物线与y轴交于点（0，-8）；
故答案是：（-4，0）、（-2，0）；（0，-8）．
点评 本题考查了抛物线与x轴的交点．求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标，令y=0，即ax2+bx+c=0，解关于x的一元二次方程即可求得交点横坐标．
练习册系列答案
相关题目
如图，∠ABC为直角，BC长为3，AB长为4，AF长为12，正方形的面积为169，求三角形AFC的面积．
如图，矩形AEHC是由三个全等矩形拼成的，AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N，设△BPQ、△DKM、△CNH的面积依次为S1、S2、S3．若S1+S3=10，则S2的值为4．
如图，点E是正方形ABCD对角线BD上一个动点，以CE为腰作等腰直角三角形ECF，使∠ECF=90°，点E在BD上移动时（与B，D都不重合），判断△DEF的形状？为什么？
如图，已知线段AB，按下列要求作图：分别以点A，B为圆心，以任意长为半径（大于AB的一半）作弧，两弧相交于点C，D．
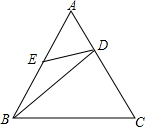如图，在等边角形ABC中，点D，E分别在AC，AB边上，且$\frac{AD}{AC}$=$\frac{1}{3}$，AE=BE，接DE，BD．求证：∠AED=∠CBD．
如图，直线1经过矩形ABCD的对称中心O，分别过点A和点C作直线1的垂线，垂足分别为E和F．求证：OE=OF．
C. 
D. 