Question

如图，梯形ABCD中，AD∥BC，E为BC上任意一点，连接AE、DE、G₁、G₂、G₃分别为△ABE，△ADE，△DEC的重心，BC=2AD=12，梯形的高为6，则△G₁G₂G₃的面积为

 

．

Answer 1

考点：三角形的重心,梯形

专题：

分析：首先连接AG₁，并延长交BC于点F，连接DG₃，并延长交BC于点K，连接EG₂，并延长交AD于点Q，交G₁G₃于点P，由G₁、G₂、G₃分别为△ABE，△ADE，△DEC的重心，易证得AD∥FK∥G₁G₃，且AD=FK=G₁G₃=6，又由G₂Q=

1

3

EQ，EP：EQ=G₃K：DK=1：3，可求得△G₁G₂G₃的高，继而求得△G₁G₂G₃的面积．

解答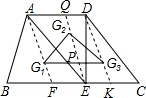：解：连接AG₁，并延长交BC于点F，连接DG₃，并延长交BC于点K，连接EG₂，并延长交AD于点Q，交G₁G₃于点P，
∵G₁、G₂、G₃分别为△ABE，△ADE，△DEC的重心，
∴AD∥FK∥G₁G₃，EF=

1

2

BE，CK=

1

2

EC，
∴FK=BE+EC=

1

2

BE+

1

2

EC=

1

2

BC，
∵BC=2AD=12，
∴FK=AD，
∴四边形AFKD是平行四边形，
∴AD=FK=G₁G₃=6，
∵G₂Q=

1

3

EQ，EP：EQ=G₃K：DK=1：3，
即EP=

1

3

EQ，
∴G₂P=

1

3

EQ，
∵梯形的高为6，
∴△G₁G₂G₃的高为：

1

3

×6=2，
∴△G₁G₂G₃的面积为：

1

2

×6×2=6．
故答案为：6．

点评：此题考查了三角形重心的性质、平行线的性质以及平行四边形的性质与判定．此题难度较大，注意掌握辅助线的作法，注意数形结合思想的应用．