题目内容
等腰△ABC中,AB=AC=13,一边上的高为5,求底边BC的长.
考点:勾股定理,等腰三角形的性质
专题:
分析:分两种情况:高在△ABC的内部;高在△ABC的外部;根据勾股定理先求得AD,再根据线段的和差求得BD,再根据勾股定理求得底边BC的长.
解答: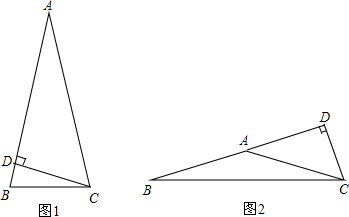 解:如图1,若高在△ABC的内部,
解:如图1,若高在△ABC的内部,
∵在△ACD中,AB=AC=13,高CD=5,
∴AD=
=12,
∴BD=AB-AD=13-12=1,
∴在△BCD中,BC=
=
;
如图2,若高在△ABC的外部,
∵在△ACD中,AB=AC=13,高CD=5,
∴AD=
=12,
∴BD=AB+AD=13+12=25,
∴在△BCD中,BC=
=5
.
故底边BC的长是
或5
.
 解:如图1,若高在△ABC的内部,
解:如图1,若高在△ABC的内部,∵在△ACD中,AB=AC=13,高CD=5,
∴AD=
| 132-52 |
∴BD=AB-AD=13-12=1,
∴在△BCD中,BC=
| 52+12 |
| 26 |
如图2,若高在△ABC的外部,
∵在△ACD中,AB=AC=13,高CD=5,
∴AD=
| 132-52 |
∴BD=AB+AD=13+12=25,
∴在△BCD中,BC=
| 52+252 |
| 26 |
故底边BC的长是
| 26 |
| 26 |
点评:本题考查了勾股定理和等腰三角形的性质.注意熟练运用勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
相关题目
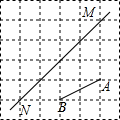 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A,B,M,N均在小正方形的顶点上.在方格纸中,画出四边形ABCD(四边形的各定点均在小正方形的顶点上),使四边形ABCD是一直线MN为对称轴对称的图形,点A的对称点为点D,点B的对称点为点C.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A,B,M,N均在小正方形的顶点上.在方格纸中,画出四边形ABCD(四边形的各定点均在小正方形的顶点上),使四边形ABCD是一直线MN为对称轴对称的图形,点A的对称点为点D,点B的对称点为点C.