题目内容
20.若菱形的一条对角线的长为6,面积为24,则这个菱形的边长为5.分析 由菱形的性质得出AB=BC=CD=DA,OA=OC=$\frac{1}{2}$AC=3,OB=OD=$\frac{1}{2}$BD,AC⊥BD,由菱形的面积求出BD,得出OB,根据勾股定理求出AB即可.
解答 解:如图所示: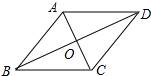 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,OA=OC=$\frac{1}{2}$AC=3,OB=OD=$\frac{1}{2}$BD,AC⊥BD,
∴菱形的面积=$\frac{1}{2}$AC•BD=24,
∴BD=8,
∴OB=$\frac{1}{2}$BD=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5;
故答案为:5.
点评 本题考查了菱形的性质、菱形面积的计算以及勾股定理;熟练掌握菱形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
8.下列4个分式:①$\frac{a+3}{{a}^{2}+3}$,②$\frac{x-y}{{x}^{2}-{y}^{2}}$,③$\frac{m}{2{m}^{2}n}$,④$\frac{2}{m+1}$中,最简分式有( )
| A. | ①④ | B. | ①② | C. | ①③ | D. | ②④ |
12.下列各式中,属于最简二次根式的是( )
| A. | $\sqrt{20}$ | B. | $\sqrt{19}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{1}{5}}$ |
 如图所示,已知渔船A在海上航行,发现一个小岛B,在渔船上测得小岛在船的北偏东37°方向上.在小岛上看,渔船在小岛的什么方向上?
如图所示,已知渔船A在海上航行,发现一个小岛B,在渔船上测得小岛在船的北偏东37°方向上.在小岛上看,渔船在小岛的什么方向上?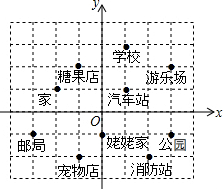 下图中标明了小红家附近的一些地方,建立平面直角坐标系如图.
下图中标明了小红家附近的一些地方,建立平面直角坐标系如图.