题目内容
19．已知M=$\root{m-4}{m+3}$是m+3的算术平方根，N=$\root{2m-4n+3}{n-2}$是n-2的立方根，试求M-N的值．分析 根据算术平方根及立方根的定义，求出M、N的值，代入可得出M-N的平方根．
解答 解：因为M=$\root{m-4}{m+3}$是m+3的算术平方根，N=$\root{2m-4n+3}{n-2}$是n-2的立方根，
所以可得：m-4=2，2m-4n+3=3，
解得：m=6，n=3，
把m=6，n=3代入m+3=9，n-2=1，
所以可得M=3，N=1，
把M=3，N=1代入M-N=3-1=2．
点评 本题考查了立方根、平方根及算术平方根的定义，属于基础题，求出M、N的值是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
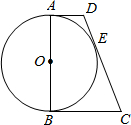如图，在直角梯形ABCD中，AD∥BC，∠A=∠B=90°，BC=4AD．AB为⊙O的直径，OA=2，CD与⊙O相切于点E．求CD的长．
如图所示，已知渔船A在海上航行，发现一个小岛B，在渔船上测得小岛在船的北偏东37°方向上．在小岛上看，渔船在小岛的什么方向上？