题目内容
13. 已知在等腰三角形ABC中,D是BC边上一点,DE⊥AB,DF⊥AC,E,F分别为垂足,若DF+DE=2$\sqrt{2}$,△ABC的面积为$\sqrt{24}$+$\sqrt{8}$,求AB的长.
已知在等腰三角形ABC中,D是BC边上一点,DE⊥AB,DF⊥AC,E,F分别为垂足,若DF+DE=2$\sqrt{2}$,△ABC的面积为$\sqrt{24}$+$\sqrt{8}$,求AB的长.
分析 直接利用△ABC的面积=S△ABD+S△ADC进而求出AB的长即可.
解答  解:连接AD,
解:连接AD,
∵在等腰三角形ABC中,DE⊥AB,DF⊥AC,
∴△ABC的面积=S△ABD+S△ADC=$\frac{1}{2}$AB(DE+DF)=$\frac{1}{2}$AB×2$\sqrt{2}$=$\sqrt{24}$+$\sqrt{8}$,
解得:AB=2$\sqrt{3}$+2.
点评 此题主要考查了二次根式的应用以及等腰三角形的性质,将△ABC分割为两部分是解题关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
2.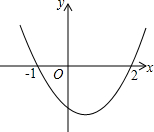 如图,抛物线y=ax2+bx+c与x轴的交点坐标是(-1,0)与(2,0),若x1,x2 (x1<x2)是方程ax2+bx+c=n(c<n<0)的两个实数根,则x1,x2的取值范围是( )
如图,抛物线y=ax2+bx+c与x轴的交点坐标是(-1,0)与(2,0),若x1,x2 (x1<x2)是方程ax2+bx+c=n(c<n<0)的两个实数根,则x1,x2的取值范围是( )
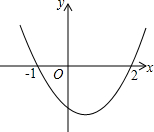 如图,抛物线y=ax2+bx+c与x轴的交点坐标是(-1,0)与(2,0),若x1,x2 (x1<x2)是方程ax2+bx+c=n(c<n<0)的两个实数根,则x1,x2的取值范围是( )
如图,抛物线y=ax2+bx+c与x轴的交点坐标是(-1,0)与(2,0),若x1,x2 (x1<x2)是方程ax2+bx+c=n(c<n<0)的两个实数根,则x1,x2的取值范围是( )| A. | x1<-1,x2>2 | B. | -1<x1<0<x2 | C. | x1<0<x2<2 | D. | -1<x1<0且0<x2<2 |
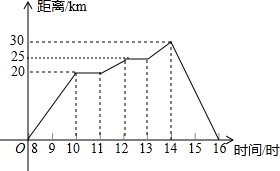 假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.
假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.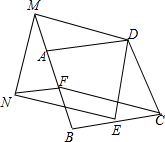 如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.
如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF. 如图,有一幅长方形山水画,它的长为90cm,宽为50cm,现在需要它的四周加装一个木框,由于悬挂位置的限制,装上后整体周长不能超过320cm,那么加装的木框条的最大宽度是多少?
如图,有一幅长方形山水画,它的长为90cm,宽为50cm,现在需要它的四周加装一个木框,由于悬挂位置的限制,装上后整体周长不能超过320cm,那么加装的木框条的最大宽度是多少?