题目内容
10.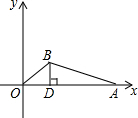 如图,在直角坐标系中,点A的坐标是(12,0),动直线OB与AB相交于点B,且BD⊥x轴于D,BD=3,则△OAB的周长的最小值是12+6$\sqrt{5}$.
如图,在直角坐标系中,点A的坐标是(12,0),动直线OB与AB相交于点B,且BD⊥x轴于D,BD=3,则△OAB的周长的最小值是12+6$\sqrt{5}$.
分析 OA长度已知,只需求折线段OBA的长度最小值即可;由于B点到OA的距离是定值,因此可以过B点作OA的平行线l,问题就转化为“牛喝水问题”.
解答 解:过点B作l∥OA,设O点关于l对称的点为C,连接AC,则AC的长度为折线段OBA的最小值,如图,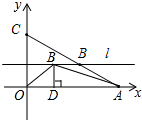
∵BD⊥OA,BD=3,
∴C点的坐标为(0,6),
由勾股定理可求得AC=$6\sqrt{5}$,
∴△OAB的周长的最小值12+6$\sqrt{5}$,
故答案为12+6$\sqrt{5}$.
点评 本题主要考查了轴对称的性质、对称法求最短路径、勾股定理等知识点,命题新颖,难度中等,是一道好题.本题表面看是一道“特别”的最值问题,实际上稍作分析即可发现就是传统的牛喝水问题,看出这一点是解答本题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
2.等腰三角形的一个外角等于130°,则这个等腰三角形的底角为( )
| A. | 65° | B. | 50° | C. | 65°或40° | D. | 50°或65° |
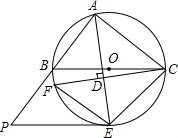 如图,△ABC是⊙O的内接三角形,BC是⊙O的直径,AE是⊙O的弦,点F是弧BE上一点,且AE⊥CF,垂足是D,⊙O的切线PE交AB的延长线于点P,
如图,△ABC是⊙O的内接三角形,BC是⊙O的直径,AE是⊙O的弦,点F是弧BE上一点,且AE⊥CF,垂足是D,⊙O的切线PE交AB的延长线于点P, 如图,已知AB∥CD,CN是∠BCE的平分线.
如图,已知AB∥CD,CN是∠BCE的平分线. 如图,在△ABC中点D、E分别在边AB、AC上,请添加一个条件:∠AEB=∠B(答案不唯一),使△ABC∽△AED.
如图,在△ABC中点D、E分别在边AB、AC上,请添加一个条件:∠AEB=∠B(答案不唯一),使△ABC∽△AED.