题目内容
6张扑克牌正面分别是1,2,3,4,5,6,将其顺序打乱,正面朝下,在其背面分别写上1,2,3,4,5,6,则每一张牌的正、反两面的差是奇数与偶数的情况是( )
| A、奇数可能性大 |
| B、偶数可能性大 |
| C、机会均等 |
| D、无法判断 |
考点:可能性的大小
专题:
分析:从反面人手,设这6个数两两都不相等,利用|ai-bi|与ai-bi(i=1,2,3,4,5,6)的奇偶性相同,引入字母进行推理证明.
解答:解:设6张卡片正面写的数是a1、a2、a3、a4、a5、a6,反面写的数对应为b1、b2、b3、b4、b5、b6,则这6张卡片正面写的数与反面写的数的绝对值分别为|a1-b1|,|a2-b2|,|a3-b3|,|a4-b4|,|a5-b5|,|a6-b6|.设这6个数两两都不相等,则它们只能取0,1,2,3,4,5这6个值.
于是|a1-b1|+|a2-b2|+|a3-b3|+|a4-b4|+|a5-b5|+|a6-b6|=0+1+2+3+4+5=15是个奇数.
另一方面,|ai-bi|与ai-bi(i=1,2,3,4,5,6)的奇偶性相同.
所以|a1-b1|+|a2-b2|+|a3-b3|+|a4-b4|+|a5-b5|+|a6-b6|与(a1-b1)+(a2-b2)+(a3-b3)+(a4-b4)+(a5-b5)+(a6-b6)=(a1+a2+a3+a4+a5+a6)-(b1+b2+b3+b4+b5+b6)=(1+2+3+4+5+6)-(1+2+3+4+5+6)=O的奇偶性相同,机会均等;
故选C.
于是|a1-b1|+|a2-b2|+|a3-b3|+|a4-b4|+|a5-b5|+|a6-b6|=0+1+2+3+4+5=15是个奇数.
另一方面,|ai-bi|与ai-bi(i=1,2,3,4,5,6)的奇偶性相同.
所以|a1-b1|+|a2-b2|+|a3-b3|+|a4-b4|+|a5-b5|+|a6-b6|与(a1-b1)+(a2-b2)+(a3-b3)+(a4-b4)+(a5-b5)+(a6-b6)=(a1+a2+a3+a4+a5+a6)-(b1+b2+b3+b4+b5+b6)=(1+2+3+4+5+6)-(1+2+3+4+5+6)=O的奇偶性相同,机会均等;
故选C.
点评:本题考查的是可能性大小的判断,解决这类题目要注意具体情况具体对待.用到的知识点为:可能性等于所求情况数与总情况数之比.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
下面四句关于约数和倍数的话中正确的是( )
| A、正整数a和b的最小公倍数一定小于ab |
| B、正整数a和b的最大公约数一定不大于a |
| C、正整数a和b的最小公倍数一定不小于ab |
| D、正整数a和b的最大公约数一定大于a |
圆的直径是13cm,如果直线与圆心的距离为4.5cm,那么直线与圆公共点有( )
| A、1个 | B、2个 | C、3个 | D、0个 |
 如图,△ABE是边长为21的正三角形.已知四边形BCDE的周长是△ABE周长的两倍.则五边形ABCDE的周长是( )
如图,△ABE是边长为21的正三角形.已知四边形BCDE的周长是△ABE周长的两倍.则五边形ABCDE的周长是( )| A、137 | B、147 |
| C、157 | D、167 |
某市2011年9月份的平均房价是每平方米6800元,比2008年同期的房价平均每平方米上涨了3000元,假设这三年该市房价的平均增长率都是x,则关于x的方程是( )
| A、(1+x)3=3000 |
| B、3000(1+x)3=6800 |
| C、(6800-3000)(1+x)2=6800 |
| D、(6800-3000)(1+x)3=6800 |
 若现在需要在电话中告诉你的同学如图的图形,你将怎么说?提供两种.
若现在需要在电话中告诉你的同学如图的图形,你将怎么说?提供两种.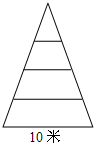 如图,是一轴截面为等腰三角形的古塔,塔基圆直径为10米,塔共四层,每层高3米,天意广告公司欲沿塔面悬挂一幅公益广告条幅,要求条幅不能铺在地面上,也不能高于塔顶,则条幅的最大长度为
如图,是一轴截面为等腰三角形的古塔,塔基圆直径为10米,塔共四层,每层高3米,天意广告公司欲沿塔面悬挂一幅公益广告条幅,要求条幅不能铺在地面上,也不能高于塔顶,则条幅的最大长度为 如图,AB是⊙O的直径,点E是
如图,AB是⊙O的直径,点E是
 如图,动物园内有两条游览线路l1、l2相交于点O,A、B是位于l1、l2上的两个电瓶车站,现准备在∠AOB内设置一个饮料供应点,要求饮料供应点P满足到A、B两个电瓶车站的距离相等,而且P到两条游览线路l1、l2的距离也相等,请用尺规作图作出点P(不写作法,保留作图痕迹).
如图,动物园内有两条游览线路l1、l2相交于点O,A、B是位于l1、l2上的两个电瓶车站,现准备在∠AOB内设置一个饮料供应点,要求饮料供应点P满足到A、B两个电瓶车站的距离相等,而且P到两条游览线路l1、l2的距离也相等,请用尺规作图作出点P(不写作法,保留作图痕迹).