题目内容
12. 如图,△ABC是等腰直角三角形,点O是斜边BC的中点,点E在AC上,点D在AB上,∠DOE=45°.若BD=9,CE=8,求DE的长.
如图,△ABC是等腰直角三角形,点O是斜边BC的中点,点E在AC上,点D在AB上,∠DOE=45°.若BD=9,CE=8,求DE的长.
分析 由等腰直角三角形的性质得出AB=AC,∠A=90°,∠B=∠C=45°,BO=CO,由角的关系证出∠BDO=∠COE,得出△BDO∽△COE,得出对应边成比例求出BO,得出BC,再由等腰直角三角形的性质求出AB=AC=12,得出AD、AE的长,然后由勾股定理求出DE即可.
解答 解:连接DE,如图所示: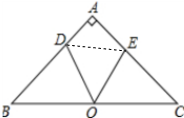
∵△ABC是等腰直角三角形,点O是斜边BC的中点,
∴AB=AC,∠A=90°,∠B=∠C=45°,BO=CO,
∴∠DOB+∠BDO=135°,
∵∠DOE=45°,
∴∠DOB+∠COE=135°,
∴∠BDO=∠COE,
∴△BDO∽△COE,
∴$\frac{BD}{CO}=\frac{BO}{EC}$,即$\frac{9}{BO}=\frac{BO}{8}$,
解得:BO=6$\sqrt{2}$,
∴BC=2BO=12$\sqrt{2}$,
∴AB=AC=$\frac{\sqrt{2}}{2}$BC=12,
∴AD=AB-BD=3,AE=AC-EC=4,
∴DE=$\sqrt{{3}^{2}+{4}^{2}}$=5.
点评 本题考查了等腰直角三角形的性质、相似三角形的判定与性质、勾股定理;熟练掌握等腰直角三角形的性质,证明三角形相似得出比例式是解决问题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
7.多项式2x-3y+4+3kx+2ky-k中没有含y的项,则k应取( )
| A. | k=$\frac{3}{2}$ | B. | k=0 | C. | k=-$\frac{2}{3}$ | D. | k=4 |
3. 如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发,以同样的速度沿边BC、DC向点C运动.下列四个结论:①AE=AF;②∠CEF=∠CFE;③当E、F分别是边BC、DC的中点时,EF=$\sqrt{3}$BE;④当E、F分别是边BC、DC的中点时,△AEF的面积最大,其中,正确的有( )
如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发,以同样的速度沿边BC、DC向点C运动.下列四个结论:①AE=AF;②∠CEF=∠CFE;③当E、F分别是边BC、DC的中点时,EF=$\sqrt{3}$BE;④当E、F分别是边BC、DC的中点时,△AEF的面积最大,其中,正确的有( )
 如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发,以同样的速度沿边BC、DC向点C运动.下列四个结论:①AE=AF;②∠CEF=∠CFE;③当E、F分别是边BC、DC的中点时,EF=$\sqrt{3}$BE;④当E、F分别是边BC、DC的中点时,△AEF的面积最大,其中,正确的有( )
如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发,以同样的速度沿边BC、DC向点C运动.下列四个结论:①AE=AF;②∠CEF=∠CFE;③当E、F分别是边BC、DC的中点时,EF=$\sqrt{3}$BE;④当E、F分别是边BC、DC的中点时,△AEF的面积最大,其中,正确的有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
17.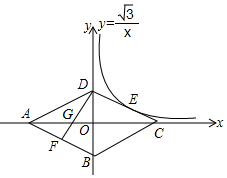 已知如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
已知如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
 已知如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
已知如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=$\frac{\sqrt{3}}{x}$(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\sqrt{3}$+2 | C. | 2$\sqrt{3}$+1 | D. | $\frac{3\sqrt{3}}{2}$+1 |
4. 如图,已知∠A=∠D,AF=CD,那么要得到△ABC≌△DEF,还应该给出的条件是( )
如图,已知∠A=∠D,AF=CD,那么要得到△ABC≌△DEF,还应该给出的条件是( )
 如图,已知∠A=∠D,AF=CD,那么要得到△ABC≌△DEF,还应该给出的条件是( )
如图,已知∠A=∠D,AF=CD,那么要得到△ABC≌△DEF,还应该给出的条件是( )| A. | AB=EF | B. | ∠E=∠B | C. | CD=AF | D. | ED=BC |