题目内容
3.如果不等式组$\left\{\begin{array}{l}x-a>0\\ x+b<0\end{array}\right.$的解集是-1<x<2,那么ab=1.分析 先用a,b表示出不等式组的解集,再根据不等式组的解集为-1<x<2求出a,b的值,代入代数式进行计算即可.
解答 解:$\left\{\begin{array}{l}x-a>0①\\ x+b<0②\end{array}\right.$,由①得,x>a,由②得,x<-b,
∵不等式组的解集为-1<x<2,
∴a=-1,b=-2,
∴ab=(-1)-2=1.
故答案为:1.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
18.不等式组$\left\{\begin{array}{l}x-1>0\\-x≥-2\end{array}\right.$的解集正确的是( )
| A. | 1<x≤2 | B. | x≥2 | C. | x<1 | D. | 无 |
8.合肥市某商场为做好“家电下乡”的惠民服务,决定从厂家购进甲、乙、丙三种不同型号的电视机108台,其中甲种电视机的台数是丙种的4倍,购进三种电视机的总金额不超过147000元,已知甲、乙、丙三种型号的电视机的出厂价格和售出后每台的利润如下表:
(1)求该商场至少购买丙种电视机多少台?
(2)若要求甲种电视机的台数不超过乙种电视机的台数,且使售出后所获利润最高,请设计进货方案,并求出售出后的最高利润.
| 型号 | 甲 | 乙 | 丙 |
| 出厂价(元/台) | 1000 | 1500 | 2000 |
| 每台利润(元/台) | 200 | 200 | 300 |
(2)若要求甲种电视机的台数不超过乙种电视机的台数,且使售出后所获利润最高,请设计进货方案,并求出售出后的最高利润.
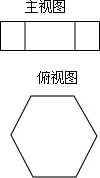 如图是一个直六棱柱的不完整的三视图,其中主视图是一个邻边为20和8的矩形,俯视图是正六边形
如图是一个直六棱柱的不完整的三视图,其中主视图是一个邻边为20和8的矩形,俯视图是正六边形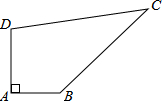 如图所示,学校内有一块四边形的空地ABCD,现计划在该空地上种植草坪经测量,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草坪皮需要400元,问需要投入多少元?
如图所示,学校内有一块四边形的空地ABCD,现计划在该空地上种植草坪经测量,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草坪皮需要400元,问需要投入多少元?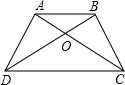 已知:如图,DA=CB,∠ADC=∠BCD.求证:∠ADB=∠BCA.
已知:如图,DA=CB,∠ADC=∠BCD.求证:∠ADB=∠BCA.