Question

15．已知：∠ACB=90°，CO=BO，等边△AOE，OF=4，DE=3，求OD的长．

Answer 1

分析 先由等边三角形的性质和直角三角形的性质，先判断出点C，E在⊙O上，得出∠ACE=30°，再判断出△OEG≌△OCF，得出∠OGE=∠OFC，进而判断出DE=DG即可．

解答 解：如图，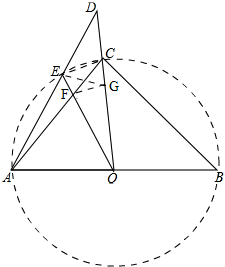


∵△AOE是等边三角形，
∴OA=OE，∠AOE=60°，
以AB为直径作⊙O，在OC上截取OG=OF，连接FG，EG，
∵OC=OB，
∴∠B=∠OCB，
∵∠OAC+∠B=90°=∠OCB+∠OCA，
∴∠OAC=∠OCA，
∴OC=OA=OE，
∴点C，E在⊙O上，
∴∠ACE=$\frac{1}{2}$∠AOE=30°，
在△OEG和△OCF中$\left\{\begin{array}{l}{OE=OC}\\{∠EOG=∠COF}\\{OF=OG}\end{array}\right.$
∴△OEG≌△OCF，
∴∠OGE=∠OFC，
∴∠EGD=∠EFC=∠AEF+∠EAF=60°+∠EAF，
∵∠OEC=∠OCE，
∴∠CEG=∠DEC+∠CDG=∠EAF+∠ACE+∠ACE=60°+∠EAF，
∴∠EGD=∠DEG，
∴DE=DG，
∴OD=OG+DG=OF+DE=7

点评 此题是四点共圆，主要考查了等边三角形的性质，直角三角形的性质，全等三角形的判定，等腰三角形的性质，解本题的关键是判断出△OEG≌△OCF，难点出作出辅助线．