题目内容
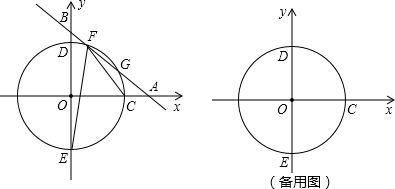
 如图,AB,AC分别是半⊙O的直径和弦,OD⊥AC于点D,过点A作半⊙O的切线AP,AP与OD的延长线交于点P.连接PC并延长与AB的延长线交于点F.
如图,AB,AC分别是半⊙O的直径和弦,OD⊥AC于点D,过点A作半⊙O的切线AP,AP与OD的延长线交于点P.连接PC并延长与AB的延长线交于点F.(1)求证:PC是半⊙O的切线;
(2)若∠CAB=30°,AB=10,求线段BF的长.
考点:切线的判定与性质,解直角三角形
专题:几何综合题,压轴题
分析:(1)连接OC,可以证得△OAP≌△OCP,利用全等三角形的对应角相等,以及切线的性质定理可以得到:∠OCP=90°,即OC⊥PC,即可证得;
(2)依据切线的性质定理可知OC⊥PE,然后通过解直角三角函数,求得OF的值,再减去圆的半径即可.
(2)依据切线的性质定理可知OC⊥PE,然后通过解直角三角函数,求得OF的值,再减去圆的半径即可.
解答: (1)证明:连接OC,
(1)证明:连接OC,
∵OD⊥AC,OD经过圆心O,
∴AD=CD,
∴PA=PC,
在△OAP和△OCP中,
,
∴△OAP≌△OCP(SSS),
∴∠OCP=∠OAP
∵PA是⊙O的切线,
∴∠OAP=90°.
∴∠OCP=90°,
即OC⊥PC
∴PC是⊙O的切线.
(2)解:∵AB是直径,
∴∠ACB=90°,
∵∠CAB=30°,
∴∠COF=60°,
∵PC是⊙O的切线,AB=10,
∴OC⊥PF,OC=OB=
AB=5,
∴OF=
=
=10,
∴BF=OF-OB=5.
 (1)证明:连接OC,
(1)证明:连接OC,∵OD⊥AC,OD经过圆心O,
∴AD=CD,
∴PA=PC,
在△OAP和△OCP中,
|
∴△OAP≌△OCP(SSS),
∴∠OCP=∠OAP
∵PA是⊙O的切线,
∴∠OAP=90°.
∴∠OCP=90°,
即OC⊥PC
∴PC是⊙O的切线.
(2)解:∵AB是直径,
∴∠ACB=90°,
∵∠CAB=30°,
∴∠COF=60°,
∵PC是⊙O的切线,AB=10,
∴OC⊥PF,OC=OB=
| 1 |
| 2 |
∴OF=
| OC |
| cos∠COF |
| 5 |
| cos60° |
∴BF=OF-OB=5.
点评:本题考查了切线的性质定理以及判定定理,以及直角三角形三角函数的应用,证明圆的切线的问题常用的思路是根据切线的判定定理转化成证明垂直的问题.

练习册系列答案
相关题目
抛物线y=2(x-3)2+4的对称轴是( )
| A、直线x=-3 |
| B、直线x=4 |
| C、直线x=3 |
| D、直线x=2 |
下列说法正确的是( )
| A、一元二次方程的一般形式是ax2+bx+c=0 | ||||
| B、方程x2=x的解是x=1 | ||||
C、一元二次方程的一般形式是ax2+bx+c=0 的根是x=
| ||||
| D、方程x(x+2)(x-3)=0的实数根有三个 |
 图中表示的不等式的解集是
图中表示的不等式的解集是 如图,三角板的直角顶点P在射线OM上,∠AOB=90°,OM是∠AOB的角平分线
如图,三角板的直角顶点P在射线OM上,∠AOB=90°,OM是∠AOB的角平分线 如图,直线L:y=-x+3与两坐标轴分别相交于点A、B.
如图,直线L:y=-x+3与两坐标轴分别相交于点A、B.