题目内容
14.某商店将进价为8元的商品按每件10元出售,每天可销售200件,现商家采用提高售价,减少进货量的方法增加利润,如果这种商品每件涨0.5元,其销量就会减少10件,那么要使利润为640元,需将售价定为( )| A. | 16元 | B. | 12元 | C. | 16元或12元 | D. | 14元 |
分析 设售价为x元,则利用每一件的销售利润×每天售出的数量=每天利润,解方程求解即可.
解答 解:设售价为x元,根据题意列方程得
(x-8)(200-$\frac{x-10}{0.5}$×10)=640,
整理得:x2-28x+192=0,
解得x1=12,x2=16.
故将每件售价定为12或16元时,才能使每天利润为640元.
又题意要求采取提高商品售价减少销售量的办法增加利润,
故应将商品的售价定为16元.
故选:A.
点评 本题考查的是一元二次方程的应用.读懂题意,找到等量关系准确的列出方程是解题的关键.

练习册系列答案
相关题目
5.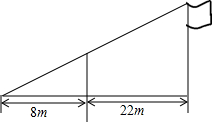 如图,小东用长3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )
如图,小东用长3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )
 如图,小东用长3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )
如图,小东用长3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为( )| A. | 12m | B. | 10m | C. | 8m | D. | 7m |
9.下面方程,不能用因式分解法求解的是( )
| A. | x2=3x | B. | (x-2)2=3x-6 | C. | 9x2+6x+1=0 | D. | (x+2)(3x-1)=5 |
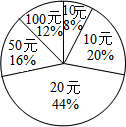 在一次捐款活动中,某班50名同学人人拿出自己的零花钱,有捐10元、20元和30元的,还有捐50元和100元的.如图反映了不同捐款数的人数比例,那么该班同学平均每人捐款31.2元.
在一次捐款活动中,某班50名同学人人拿出自己的零花钱,有捐10元、20元和30元的,还有捐50元和100元的.如图反映了不同捐款数的人数比例,那么该班同学平均每人捐款31.2元. 如图,AB为斜坡,D是斜坡AB上一点,斜坡AB的坡度为i,坡角为α,AC⊥BM于点C,下列式子:①i=AC:AB;②i=(AC-DE):EC;③i=tanα=$\frac{DE}{BE}$;④AC=i•BC,其中正确的有( )
如图,AB为斜坡,D是斜坡AB上一点,斜坡AB的坡度为i,坡角为α,AC⊥BM于点C,下列式子:①i=AC:AB;②i=(AC-DE):EC;③i=tanα=$\frac{DE}{BE}$;④AC=i•BC,其中正确的有( ) 如图,已知点M是反比例函数y=-$\frac{6}{x}$的图象上任意一点,过点M分别作x轴、y轴的垂线,垂足依次为P,Q,那么四边形OQMP的面积为6.
如图,已知点M是反比例函数y=-$\frac{6}{x}$的图象上任意一点,过点M分别作x轴、y轴的垂线,垂足依次为P,Q,那么四边形OQMP的面积为6.