Question

12．如图，已知AB是⊙O的直径，点P为圆上一点，点C为AB延长线上一点，PA=PC，∠C=30°．
（1）求证：CP是⊙O的切线．
（2）若⊙O的直径为8，求阴影部分的面积．

Answer 1

分析 （1）连接OP，由等腰三角形的性质得出∠C=∠OPA=30°，∠APC=120°，求出∠OPC=90°即可；
（2）证明△OBP是等边三角形，阴影部分的面积=扇形OBP的面积-△OBP的面积，即可得出结果．

解答 （1）证明：连接OP，如图所示：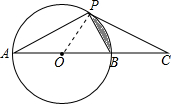
∵PA=PC，∠C=30°，
∴∠A=∠C=30°，
∴∠APC=120°，
∵OA=OP，
∴∠OPA=∠A=30°，
∴∠OPC=120°-30°=90°，
即OP⊥CP，
∴CP是⊙O的切线．
（2）解：∵AB是⊙O的直径，
∴∠APB=90°，
∴∠OBP=90°-∠A=60°，
∵OP=OB=4，
∴△OBP是等边三角形，
∴∠POC=60°，
∵OP⊥CP，
∴∠C=30°，
∴OC=2OP=2OB=8，
∴PC=$\sqrt{O{C}^{2}-O{P}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$，
∴阴影部分的面积=扇形OBP的面积-△OBP的面积=$\frac{60π•{4}^{2}}{360}$-$\frac{1}{2}$×$\frac{1}{2}$×4×4$\sqrt{3}$=$\frac{8}{3}π$-4$\sqrt{3}$．

点评 本题考查的是切线的判定、等腰三角形的性质、圆周角定理、等边三角形的判定与性质、扇形面积公式等知识；熟练掌握切线的判定．证明三角形是等边三角形是解决问题（2）的关键．